主席树总结

主席树总结

主席树一个可持久化数据结构。

什么叫可持久化数据结构？？？普通数据结构维护的是更新之后的状态，这个状态会覆盖之前的状态，使得之前的状态丢失，但可持久化数据结构并不是这样，通过建立多个不同版本的线段树，使得历史版本的线段树仍然可以查询到，更新并不会影响历史版本的状态，这种就叫可持久化线段树。

主席树其实可以维护的是历史版本的区间信息。

区间第K大

区间中小于某个值的个数

等等区间信息

可以说是非常方便的数据结构。同时可以与树上操作进行结合，进行解决某些树上问题，如树上第K小

POJ - 2104 K-th Number 区间第K小

模板题。。。查询root[l-1]到root[r]两个版本线段树之间的差异

用新版本的线段树去减去老版本的线段树，那么他们之间的信息就是他们的差值

所以查询第K小的信息就是

int query(int l,int r,int L,int R,int k){

    if (l==r)return l;

    int mid=MID(l,r);

    int tmp=tree[tree[R].l].sum-tree[tree[L].l].sum;//区间中左儿子的个数

    if (k<=tmp)query(l,mid,tree[L].l,tree[R].l,k);

    else query(mid+1,r,tree[L].r,tree[R].r,k-tmp);

}

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<vector>
#define rep(i,j,k) for (int i=j;i<=k;i++)
#define per(i,j,k) for (int i=j;i>=k;i--)
#define pb push_back
using namespace std;
const int maxx = 100005;
vector<int>v;
struct node{
  int l,r,sum;
}tree[maxx*40];
int a[maxx];
int root[maxx*40];
inline int L(int root){return root<<1;};
inline int R(int root){return root<<1|1;};
inline int MID(int l,int r){return (l+r)>>1;};
int cnt;
void insert(int l,int r,int pre,int &now,int p){
   tree[++cnt]=tree[pre];
   now=cnt;
   tree[now].sum++;
   if (l==r){
     return ;
   }
   int mid=MID(l,r);
   if (p<=mid){
     insert(l,mid,tree[pre].l,tree[now].l,p);
   }else {
     insert(mid+1,r,tree[pre].r,tree[now].r,p);
   }
}
int query(int l,int r,int L,int R,int k){
    if (l==r)return l;
    int mid=MID(l,r);
    int tmp=tree[tree[R].l].sum-tree[tree[L].l].sum;
    if (k<=tmp)query(l,mid,tree[L].l,tree[R].l,k);
    else query(mid+1,r,tree[L].r,tree[R].r,k-tmp);
}
int main(){
  int n,m;
  while(~scanf("%d%d",&n,&m)){
    memset(tree,0,sizeof(tree));
    v.clear();
    rep(i,1,n){
        scanf("%d",&a[i]);
        v.pb(a[i]);
    }
    cnt=0;
    sort(v.begin(),v.end());
    v.erase(unique(v.begin(),v.end()),v.end());
    for (int i=1;i<=n;i++){
        a[i]=lower_bound(v.begin(),v.end(),a[i])-v.begin()+1;
    }
    rep(i,1,n){
       insert(1,n,root[i-1],root[i],a[i]);
    }
    while(m--){
        int l,r,k;
        scanf("%d%d%d",&l,&r,&k);
        printf("%d
",v[query(1,n,root[l-1],root[r],k)-1]);
    }
  }
  return 0;
}

Count on a tree SPOJ – COT树上第K 小

主席树的入门题目，这道题的题意其实就是说，给你一棵树，询问在两个节点之间的路径上的区间第K小

我们如何把树上问题转换为区间问题呢？

其实DFS就可以，我们按照DFS的顺序，对线段树进行建树，那么这个树上问题就可以转换为区间问题了，

那么如何询问来表示两个节点之间的路径呢？

其实也很简单，我们建图的路径是从父亲节点到子节点。

那么其实很简单考虑一下图形

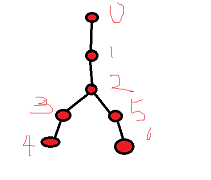
我们需要求树上第K小，但是我们知道，我们可以通过DFS序，把树上操作移植到序列操作，我们是从父亲节点到儿子节点建立的主席树。

那么我们两个不同版本的信息分别是

        

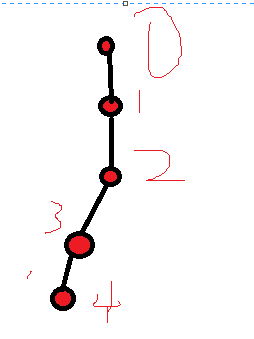
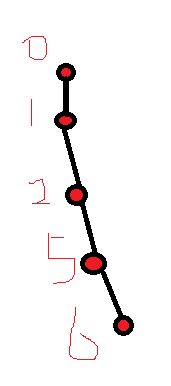
  我们如何利用这两个版本的信息，得到答案呢？？？

  我们来观察树链

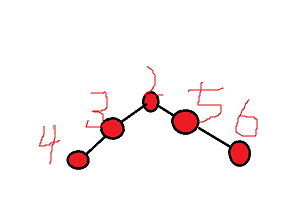
我们发现这样一个有趣的东西，我们有ans=tree[L]+tree[R]-tree[LCA(L,R)]-tree[fa(LCA(L,R))]

也就是说我们需要的信息，是新的版本的线段树+原来版本的线段树-这两棵树的公共祖先的版本的线段树-公共祖先的父亲版本的线段树。

那么这个题就变得非常简单了，只是多了一个求LCA的操作

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<vector>
#include<algorithm>
#define LL long long
#define rep(i,j,k) for(int i=j;i<=k;i++)
#define per(i,j,k) for(int i=j;i>=k;i--)
#define pb push_back
using namespace std;
const int maxx = 100005;
struct node{
   int l,r,cnt;
}tree[maxx*40];
inline int MID(int l,int r){return (l+r)>>1;};
int root[maxx*40];
int a[maxx];
int ver[maxx*2],Next[maxx*2],head[maxx];
int tot,cnt,n,m;
int t=18;
int fa[maxx],p[maxx][20],deepth[maxx];
vector<int>v;
void add(int x,int y){
   ver[++tot]=y;Next[tot]=head[x];head[x]=tot;
   ver[++tot]=x;Next[tot]=head[y];head[y]=tot;
}
void update(int l,int r,int pre,int &now,int pos){
   now=++cnt;
   tree[now]=tree[pre];
   tree[now].cnt++;
   if (l==r)return;
   int mid=(l+r)>>1;
   if (pos<=mid)
    update(l,mid,tree[pre].l,tree[now].l,pos);
   else
    update(mid+1,r,tree[pre].r,tree[now].r,pos);
}
int query(int l,int r,int L,int R,int k,int lca,int flac){
   if (l==r)return l;
   int tmp=tree[tree[R].l].cnt+tree[tree[L].l].cnt-tree[tree[lca].l].cnt-tree[tree[flac].l].cnt;
   int mid=MID(l,r);
   if (k<=tmp)
     return query(l,mid,tree[L].l,tree[R].l,k,tree[lca].l,tree[flac].l);
   else
     return query(mid+1,r,tree[L].r,tree[R].r,k-tmp,tree[lca].r,tree[flac].r);
}
void dfs(int u,int pre){
   fa[u]=pre;
   deepth[u]=deepth[pre]+1;
   p[u][0]=pre;
   update(1,n,root[pre],root[u],a[u]);
   rep(i,1,18)p[u][i]=p[p[u][i-1]][i-1];
   for (int i=head[u];i;i=Next[i]){
      int y=ver[i];
      if (y==pre)continue;
      dfs(y,u);
   }
}
int LCA(int x,int y){
   if (deepth[x]>deepth[y])swap(x,y);
   per(i,t,0){
     if (deepth[p[y][i]]>=deepth[x])y=p[y][i];
   }
   if (x==y)return y;
   per(i,t,0){
      if(p[x][i]!=p[y][i])x=p[x][i],y=p[y][i];
   }
   return p[x][0];
}
int main(){
    while(~scanf("%d%d",&n,&m)){
        int uu,vv;
        memset(head,0,sizeof(head));
        rep(i,1,n){
          scanf("%d",&a[i]);
          v.pb(a[i]);
        }
        tot=1;
        cnt=0;
        sort(v.begin(),v.end());
        v.erase(unique(v.begin(),v.end()),v.end());
        rep(i,1,n-1){
          scanf("%d%d",&uu,&vv);
          add(uu,vv);
        }
        rep(i,1,n){
          a[i]=lower_bound(v.begin(),v.end(),a[i])-v.begin()+1;
        }
        dfs(1,0);
        int k;
        while(m--){
            scanf("%d%d%d",&uu,&vv,&k);
            int lca=LCA(uu,vv);
            printf("%d
",v[query(1,n,root[uu],root[vv],k,root[lca],root[fa[lca]])-1]);
        }
    }
   return 0;
}

HDU - 5919 F - Sequence II

题意

问这个区间里面有k个不同的数,把它们第一次出现的位置从小到大排序,问第k/2个位置是什么;，

….对于主席树，我们肯定是维护一个它第一次出现的位置，并维护区间和，从而利用区间第K小得到答案。

但是我们正着思考，这个似乎是没有前缀性质的，因为L区间版本的主席树，维护的是1-L区间的数字第一出现的次数，但是