GBDT(Gradient Boosting Decision Tree，Friedman，1999)算法自提出以来，在各个领域广泛使用。从名字里可以看到，该算法主要涉及了三类知识，Gradient梯度、Boosting集成算法和 Decision Tree决策树。
该算法是GREEDY FUNCTION APPROXIMATION A GRADIENT BOOSTING MACHINE一文提出来的，它是一种基于 Gradient 的 Boosting Ensemble 模型。该算法底层基于 CART（GBDT 主要基于回归树） 和函数空间的梯度降算法，除了具有树模型的可解释性强、有效处理混合类型的特征、伸缩不变性（不需要对数据标准化）、对缺失值鲁棒等优点，还具有预测能力强、稳定性好等优势。相比于它的后继算法 XGboost/LightGBM ， GBDT 只要求模型损失函数一阶可导，凸或非凸都适用;而 XGboost/LightGBM 对损失函数的要求更为苛刻，必须一阶二阶都可导，而且要求损失函数为严格的凸函数。
GBDT 顾名思义，其基本原理包括两个核心算法思想，一个是加性增强；另一个是梯度增强。
加法模型：
最终的分类器函数形式如下：
其中，第t颗回归树，其对应的叶节点区域
。其中J为叶子节点的个数。
针对每一个叶子节点里的样本，我们求出使损失函数最小，也就是拟合叶子节点最好的的输出值
如下：
梯度增强：
大牛Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值，进而拟合一个CART回归树。第t轮的第i个样本的损失函数的负梯度表示为
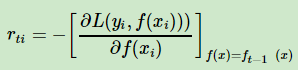
利用
可以拟合一颗CART回归树，得到了第t颗回归树，其对应的叶节点区域。其中J为叶子节点的个数。
GBDT算法：
1、回归算法
A. GBDT 回归算法在了解其基本原理之后，我们看看 GBDT 用于回归和分类的具体算法。在回归算法中，典型的损失函数为 MSE 损失
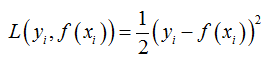
那么可得，在实际训练迭代过程中，在训练第 t 棵树的时候，我们需要将拟合的目标变量变为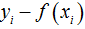
，可以看到新的目标变量即是样本的原始目标变量和截止到上一时刻模型预测输出的差值，也就是残差。
2、分类算法
GBDT 用于分类场景的时候，其核心是如何将分类问题转化为回归问题。我们以多分类的基础，阐述 GBDT 在分类中的算法过程。
假设类别数量为 K ，经过 T 轮迭代，得到 T*K 棵回归树。即在每一轮迭代的过程中，是针对样本 X 每个可能的类都训练一个分类回归树，需要建立 K 棵 1 vs. All 的回归树。
多分类中，使用的损失函数为交叉熵
也就是说，在每一轮迭代的过程中，需要建立 K 棵 1 vs. All 的回归树，且需要将叶子节点的输出(截止到 t 时刻的第 k 棵树的累积值)转化为概率,使用 Softmax 来计算
上式等价于
相比于 GBDT 回归，在分类的时候，树的输出再经过一次变换后，才进行损失函数的计算
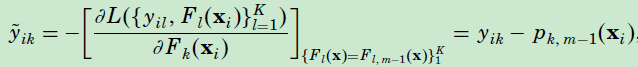
即每个样本在第 t 轮中的第 k 树的新的目标变量, 和特征向量一起构成样本。这样每一轮的迭代中，就可以拟合 k 棵回归树。新形成的k棵树，求解损失函数最小的式子如下，其中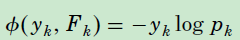
，则：
上式子难以求解，叶子节点对应的预测值（或者叫权重）可以通过一次 Newton-Raphson 操作来计算：
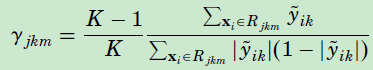
算法如下：
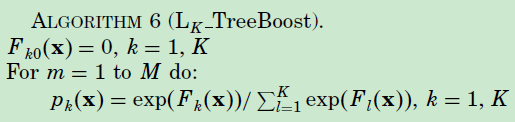
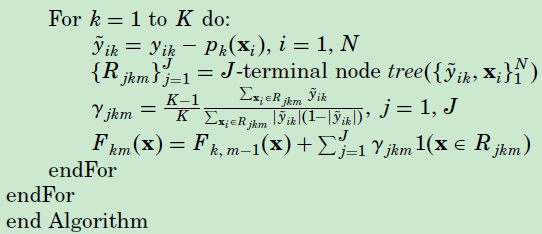
https://www.sohu.com/a/227107019_505779
https://www.cnblogs.com/pinard/p/6140514.html
这篇有个例子，https://www.cnblogs.com/ModifyRong/p/7744987.html
这篇是原文翻译，https://www.cnblogs.com/bentuwuying/p/6667267.html