P3375 【模板】KMP字符串匹配
题目描述
如题,给出两个字符串s1和s2,其中s2为s1的子串,求出s2在s1中所有出现的位置。
为了减少骗分的情况,接下来还要输出子串的前缀数组next。如果你不知道这是什么意思也不要问,去百度搜[kmp算法]学习一下就知道了。
输入输出格式
输入格式:第一行为一个字符串,即为s1(仅包含大写字母)
第二行为一个字符串,即为s2(仅包含大写字母)
输出格式:若干行,每行包含一个整数,表示s2在s1中出现的位置
接下来1行,包括length(s2)个整数,表示前缀数组next[i]的值。
输入输出样例
输入样例#1:
ABABABC ABA
输出样例#1:
1 3 0 0 1
说明
时空限制:1000ms,128M
数据规模:
设s1长度为N,s2长度为M
对于30%的数据:N<=15,M<=5
对于70%的数据:N<=10000,M<=100
对于100%的数据:N<=1000000,M<=1000
样例说明:
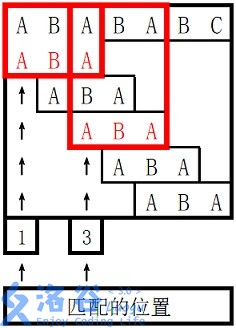
所以两个匹配位置为1和3,输出1、3
Solution
从matrix67的blog上学习了一下,
设要在A中找B,朴素的匹配方法就是从1 to len(A)每次copy一段len(B)长的和B比较
但是KMP定义了一个next数组
表示对于某个字符串S的前i个字符构成的子串,既是它的后缀又是它的前缀的字符串中(它本身除外),最长的长度记作next[i]
那么我们在朴素匹配失败时可以相当于把模式串往右移动next[i]可以了
具体见KMP算法详解-Matrix67: The Aha Moments
Codes
1 program wonder; 2 var 3 a,b:ansistring;//!!! 4 i,j,la,lb,tot:longint; 5 next:array[1..1000] of longint; 6 7 procedure iii(i:longint);//找到了 8 begin 9 writeln(i-lb+1); 10 j:=next[j]; 11 end; 12 13 begin 14 readln(a); 15 readln(b); 16 la:=length(a); 17 lb:=length(b); 18 19 next[1]:=0; 20 j:=0; 21 for i:= 2 to lb do 22 begin 23 while (j>0) and (b[i]<>b[j+1]) do j:=next[j]; 24 if b[i]=b[j+1] then j:=j+1; 25 next[i]:=j; 26 end; 27 28 j:=0; 29 for i:= 1 to la do 30 begin 31 while (j>0) and (a[i]<>b[j+1]) do j:=next[j]; 32 if a[i]=b[j+1] then inc(j); 33 if j=lb then iii(i); 34 end; 35 36 for i:= 1 to lb do write(next[i],' '); 37 end.