PAT A1127 ZigZagging on a Tree （30 分）

Suppose that all the keys in a binary tree are distinct positive integers. A unique binary tree can be determined by a given pair of postorder and inorder traversal sequences. And it is a simple standard routine to print the numbers in level-order. However, if you think the problem is too simple, then you are too naive. This time you are supposed to print the numbers in "zigzagging order" -- that is, starting from the root, print the numbers level-by-level, alternating between left to right and right to left. For example, for the following tree you must output: 1 11 5 8 17 12 20 15.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the inorder sequence and the third line gives the postorder sequence. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the zigzagging sequence of the tree in a line. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

8
12 11 20 17 1 15 8 5
12 20 17 11 15 8 5 1

　　

Sample Output:

1 11 5 8 17 12 20 15

　　

 result:

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int maxn = 33;
int n,postOrder[maxn],inOrder[maxn];
vector<vector<int> > ans(maxn); 
int level1=0;

void createTree(int inL,int inR,int postL,int postR,int level2){
    if(postR<postL || inR<inL) return ;
    int data = postOrder[postR];
    ans[level2].push_back(data);
//    printf("%d ",data);
    level1 = max(level1,level2);
    int num=0;
    while(inOrder[inL+num] != postOrder[postR]){
        num++;
    }
    // 这样生成的num指的是有num个lchild;
    createTree(inL,inL+num-1,postL,postL +num-1,level2+1);
    createTree(inL+num+1,inR,postL +num,postR - 1,level2+1);
    return ;
}


int main(){
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&inOrder[i]);
    }
    for(int i=0;i<n;i++){
        scanf("%d",&postOrder[i]);
    }
    createTree(0,n-1,0,n-1,0);
    int s = 0;
    bool flag = false;
    for(vector<vector<int> >::iterator i=ans.begin();i!=ans.end();++i){
        if(flag){
            for(vector<int>::iterator j=(*i).begin();j !=(*i).end();++j){
                printf("%d",(*j));
                s++;
                if(s<n) printf(" ");
            }
            flag=false;
        }else{
            reverse((*i).begin(),(*i).end());
            for(vector<int>::iterator j=(*i).begin(); j !=(*i).end();++j){
                printf("%d",(*j));
                s++;
                if(s<n) printf(" ");
            }
            flag=true;
        }
    }
}

收获：

此题主要的问题是如何生成蛇形层次排序法。首先想到的存储结构是按照二维数组ans[level][]保存结果。

如果以int ans[][]定义的话需要面对阈值问题，以及设计计数器问题。看题目里是没有阈值限制的，所以还需要自己设置。对于考试来说，也是可以实现的。

另外一种方式是利用vector<int>;在此题我首次体验了一下二维的vector<vector<int> >; 需要注意的是，普通二维数组需要确定第二维度的阈值；而在vector中，需要声明第一维度的阈值。而且设置阈值的方式是用小括号，而非数组形式的中括号。

对于vector<>进行迭代有两种方法，一种是用下标进行访问。使用下标访问需要结合vector<>的生成方式配合使用。一般是int i =0;i< vector.size();i++的方式；但是对于比较妖怪的存储方法，或者间断的存储方式，下标访问不是很方便。

一种是用迭代器访问，如上代码，清晰的给出了二维向量的访问方法。这里需要注意的是对于vector<>,弄清楚 front,back,begin,end四个方法的具体区别。简单说front,back可以直接引用首尾向量；begin,end返回的是vector<>首尾的迭代器。其中begin和front效果一致，但end指的是空迭代器；这也是为何遍历的时候结束条件是i!=vector.end();

使用迭代器还需要掌握一点是逆序遍历迭代器。逆序遍历有两种方法可以实现。

1）利用algorithm::reverse(a,b)先互换begin(),end();其他完全不变的方式实现。（如上代码）；

     同样的方法也可以换个写法：

// sorts vector in "normal" order  
sort(vector.begin(), vector.end());  
// sorts in reverse: puts smallest element at the end of vector 
sort(vector.rbegin(), vector.rend()); 

这是利用了vector<>自身方法的解决方案，下图是begin(),end(),rend(),rbegin()四者的关系。

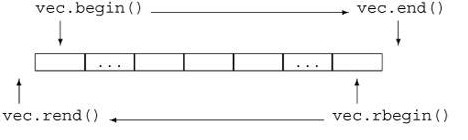
2）生成反向迭代器

for(vector<int>::reverse_iterator  j=(*i).rbegin(); j !=(*i).rend();++j){
    printf("%d",(*j));
    s++;
    if(s<n) printf(" ");
}