轻院 2180GJJ的日常之沉迷数学逆元求除法取余

题目链接：https://acm.zzuli.edu.cn/zzuliacm/problem.php?id=2180

题目大意：求数列 k⁰,k¹,k²...kⁿ的和，即等比数列的前n项和对1e9+7取余的结果。

解题思路：等比数列前N项和为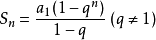，因此只要能够取余即可求得结果。利用扩展GCD求q-1关于mod的逆元然后快速幂取模计算即可。

代码：

 1 const int inf = 0x3f3f3f3f;
 2 const int maxn = 1e6 + 5;
 3 int k, n;
 4  
 5 void ext_gcd(ll a, ll b, ll &d, ll &x, ll &y){
 6     if(b == 0){
 7         d = a; x = 1; y = 0;
 8     }
 9     else{
10         ext_gcd(b, a % b, d, y, x); y -= x * (a / b);
11     }
12 }
13 ll pow_mod(ll a, ll b, ll m){
14     if(b == 0) return 1;
15     ll tmp = pow_mod(a, b / 2, m);
16     ll ans = tmp * tmp % mod;
17     if(b & 1) ans = a % mod * ans % mod;
18     return ans % mod;
19 } 
20 void solve(){
21     if(k == 1){
22         printf("%d
", (n + 1) % mod);
23         return;
24     }
25     ll a = k - 1;
26     ll b = mod, d, x, y;
27     ext_gcd(a, b, d, x, y);
28     if(x < 0) x = x + (abs(x) / mod + 1) * mod;
29     x %= mod;
30     ll tmp = pow_mod(k, n + 1, mod);
31     ll ans = (tmp * x - x) % mod ;
32     ans %= mod;
33     printf("%lld
", ans);
34 }
35 int main(){
36     int t = 1;
37     while(scanf("%d %d", &k, &n) != EOF){
38         printf("Case %d: ", t++);
39         solve();
40     }
41 }

题目：

GJJ的日常之沉迷数学

Time Limit: 1 Sec Memory Limit: 128 MB
Submit: 281 Solved: 21

Submit Status Web Board

Description

GJJ每天都要膜拜一发数学大佬，因为GJJ的数学太差了。这不，GJJ又遇到难题了，他想求助WJJ，但是WJJ这几天忙于追妹子，哪有时间给他讲题，于是GJJ求助于热爱ACM的你，Acmer们能帮帮他吗？问题是求： k^0 + k^1 +...+ k^(n) mod p (0 < k < 100， 0 <= n <= 10^9, p = 1000000007)

例如：6^0 + 6^1 +...+ 6^(10) mod 1000000007 （其中k = 6, n = 10, p = 1000000007）

Input

输入测试数据有多组，每组输入两个整数k, n

Output

每组测试数据输出：Case #: 计算结果

Sample Input

2 1 6 10

Sample Output

Case 1: 3 Case 2: 72559411