HDU 6185 Covering

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6185

题目大意：给一个N*4的方格矩阵，现在用1*2或2*1的方格铺满它，问有多少种方法。结果对1e9+7取模。N<=1e18

解题思路：一看N很大就能够想到需要一个logN级别的算法。这个题目与我昨天写的这个题目：http://www.cnblogs.com/bolderic/p/7487674.html 基本上一样，但是不同的是N和M的取值。如果依然用状态压缩的动态规划解法显然会超时。但是这样考虑，对于N列矩阵来说，放的方法实际上有五种分别是：

　　　　　　　　　

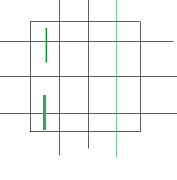
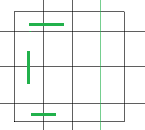
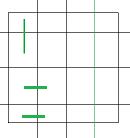
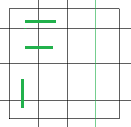
那么可以构造四个形状来递推：

　　　　　　

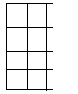
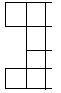
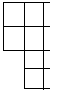
从前到后设为A,B,C,D，则有：

A(n) = A(n - 1) + B(n - 1) + 2D(n - 1) + A(n - 2), A(0) = 1, A(1) = 1

B(n) = A(n - 1) + C(n - 1), B(0) = 0, B(1) = 1

C(n) = B(n - 1), C(0)= 0, C(1) = 0

D(n) = D(n - 1)  + A（n - 1）, D(0) = 0, D(1) = 1

然后就可以构造一个5*5的矩阵计算：

A(n)　　 1 1 0 2 1　　A(n - 1)

B(n)　　 1 0 1 0 0　　B(n - 1)

C(n)　=   0 1 0 0 0　*  C(n - 1)

D(n)　　 1 0 0 1 0　　D(n - 1)

A(n - 1)   1 0 0 0 0　　A(n - 2)

代码：

typedef vector<ll> vec;
typedef vector<vec> mat;
ll n;

mat mul(mat &A, mat &B){
    mat C(A.size(), vec(B[0].size()));
    for(int i = 0; i < A.size(); i++){
        for(int k = 0; k < B.size(); k++){
            for(int j = 0; j < B[0].size(); j++){
                C[i][j] = (C[i][j] + A[i][k] % mod * B[k][j]) % mod;
            }
        }
    }
    return C;
}
mat pow(mat A, ll n){
    mat B(A.size(), vec(A.size()));
    for(int i = 0; i < A.size(); i++){
        B[i][i] = 1;
    }
    while(n > 0){
        if(n & 1) B = mul(B, A);
        A = mul(A, A);
        n >>= 1;
    }
    return B;
}
void solve(){
    mat A(5, vec(5));
    A[0][0] = 1; A[0][1] = 1; A[0][2] = 0; A[0][3] = 2; A[0][4] = 1;
    A[1][0] = 1; A[1][1] = 0; A[1][2] = 1; A[1][3] = 0; A[1][4] = 0;
    A[2][0] = 0; A[2][1] = 1; A[2][2] = 0; A[2][3] = 0; A[2][4] = 0;
    A[3][0] = 1; A[3][1] = 0; A[3][2] = 0; A[3][3] = 1; A[3][4] = 0;
    A[4][0] = 1; A[4][1] = 0; A[4][2] = 0; A[4][3] = 0; A[4][4] = 0;
    A = pow(A, n - 1);
    ll ans = A[0][0] + A[0][1] + A[0][3] + A[0][4];
    printf("%lld
", ans % mod);
}
int main(){
    while(scanf("%lld", &n) != EOF){
        solve();
    }
}

题目：

Covering

Time Limit: 5000/2500 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 643    Accepted Submission(s): 281

Problem Description

Bob's school has a big playground, boys and girls always play games here after school.

To protect boys and girls from getting hurt when playing happily on the playground, rich boy Bob decided to cover the playground using his carpets.

Meanwhile, Bob is a mean boy, so he acquired that his carpets can not overlap one cell twice or more.

He has infinite carpets with sizes of 1×2 and 2×1, and the size of the playground is 4×n.

Can you tell Bob the total number of schemes where the carpets can cover the playground completely without overlapping?

 

Input

There are no more than 5000 test cases. 

Each test case only contains one positive integer n in a line.

1≤n≤1018

 

Output

For each test cases, output the answer mod 1000000007 in a line.

 

Sample Input

1 2

 

Sample Output

1 5

 

Source

2017ACM/ICPC广西邀请赛-重现赛（感谢广西大学）