经网友jokeren提醒,后面给出的代码虽然可以AC原题,但存在bug,主要是在矩形覆盖情况的判断上处理的不够完全。
看似挺复杂的,但是仔细分析一下可以化简:
首先,不用枚举周长,因为更长的周长总是能够围成更大的面积,所以只要考虑如何在周长为L的前提下枚举面积就行了。
下图中,用蓝色线框表示跑马的路线,灰色矩形表示臭水塘。
假设可以穿越臭水塘,那么:圈地面积=蓝矩形面积 - 蓝矩形内部的灰色矩形面积。

现在不让穿越臭水塘,为了维持面积不变,就需要绕着臭水塘走:
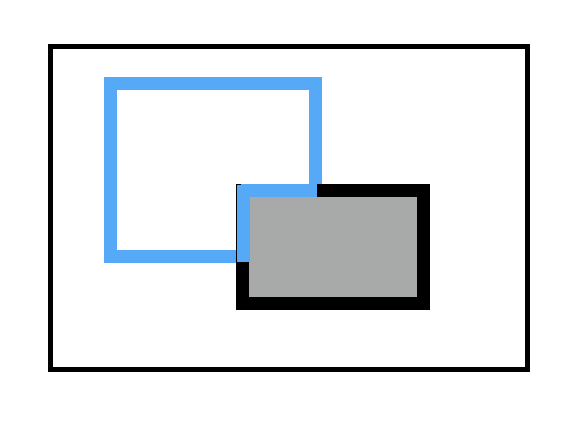
注意:绕路以后,面积不变。
上面这个例子说明:不管你怎么跑马,圈出什么形状的地,都可以转化成一个蓝矩形和黑矩形覆盖的情况(当然如果二者不相交就更简单了)。
所以,不用去考虑圈地的形状,只需要枚举蓝矩形面积,然后减掉臭水塘的面积,就是圈地的面积。
上面的转化看上去很美好,但问题来了,虽然面积不变,但周长可能会变化。仔细分析,一共有这几种情况:
情况I:绕路以后,周长不变:
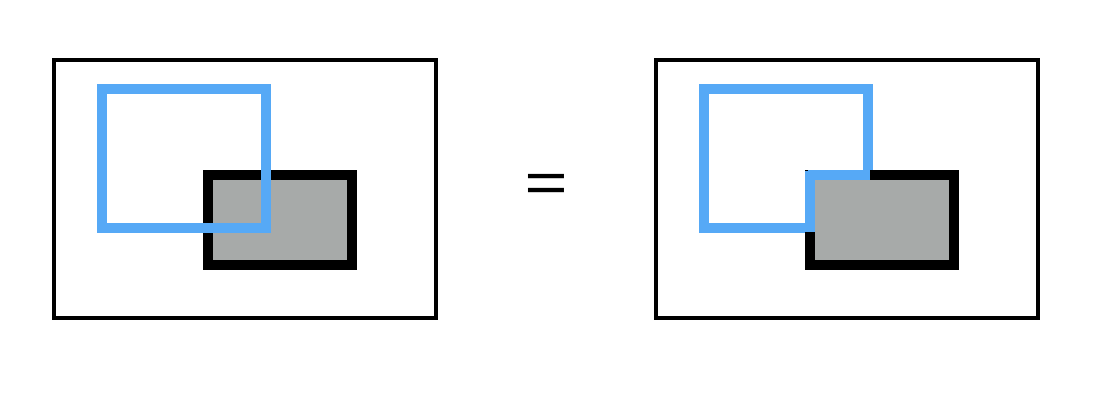
情况II:绕路以后,周长增加:
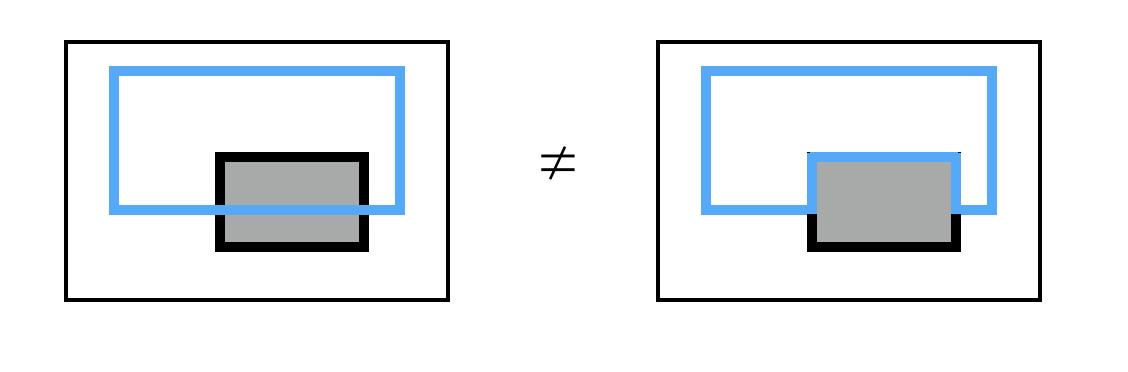
情况III:绕路以后,周长变小:
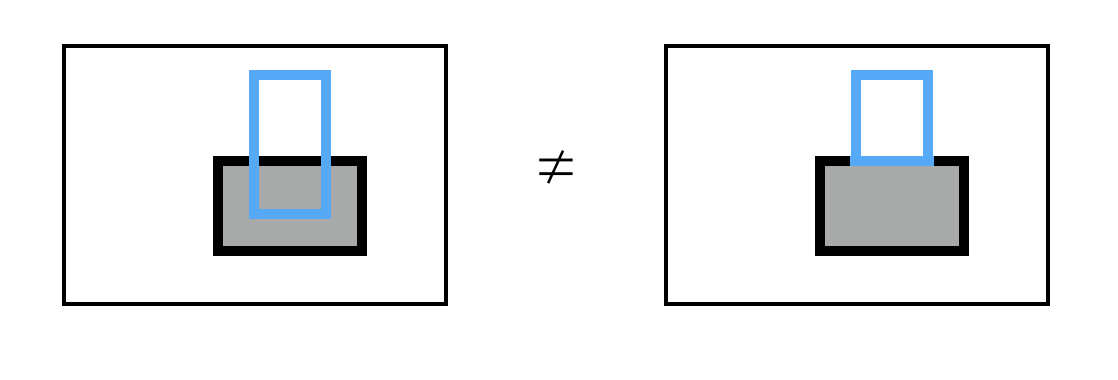
情况IV:矩形不相交,无变化:
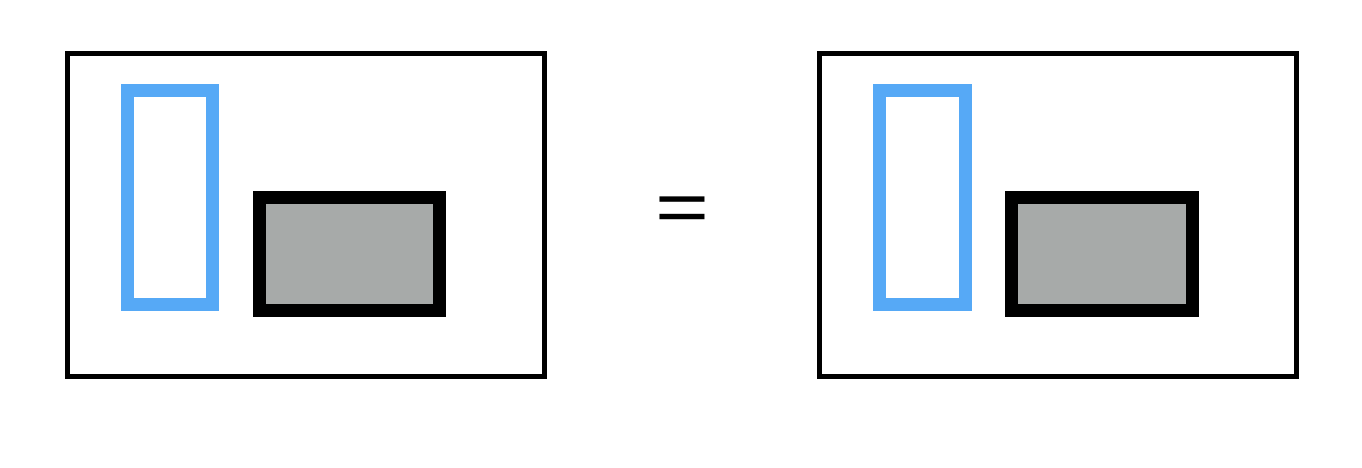
情况V:蓝矩形覆盖灰矩形,无变化:
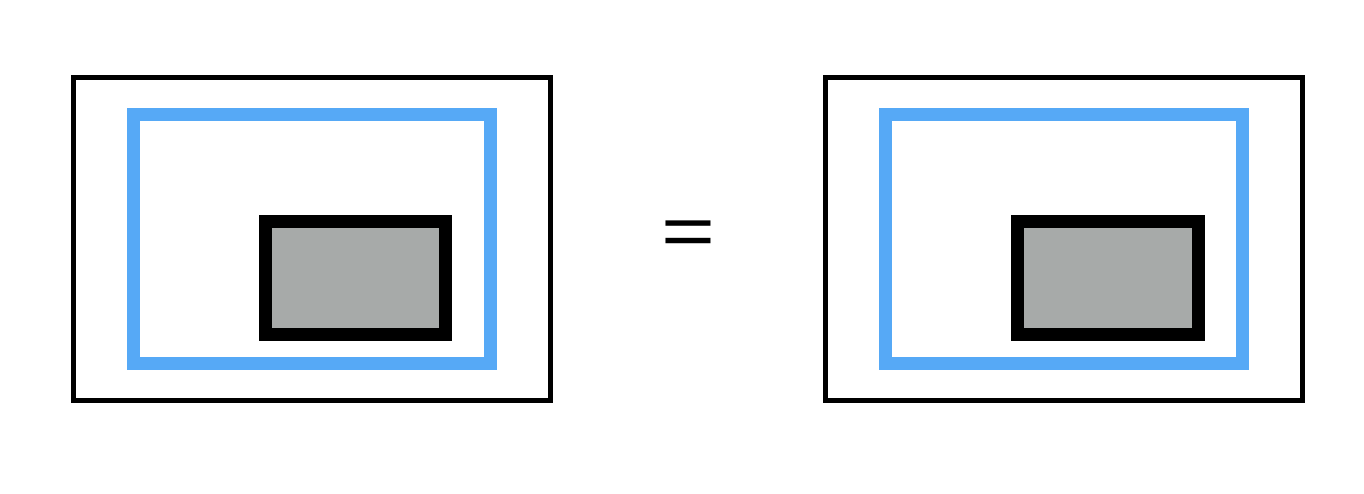
情况VI:这种情况是不合法的,遇到就直接跳过吧:

情况I、IV、V最好,直接计算即可
情况II不考虑,因为周长爆了,不满足周长等于L的条件
情况III也不考虑,因为当计算两个矩形不相交的时候会覆盖到这种情景。
所以,只需要考虑情况I、IV、V即可,是不是瞬间变简单了!
那如何判断是情况I、IV、V呢?
仔细观察,可以发现矩形的重叠情况跟灰矩形在蓝矩形内部的点的数量有关:
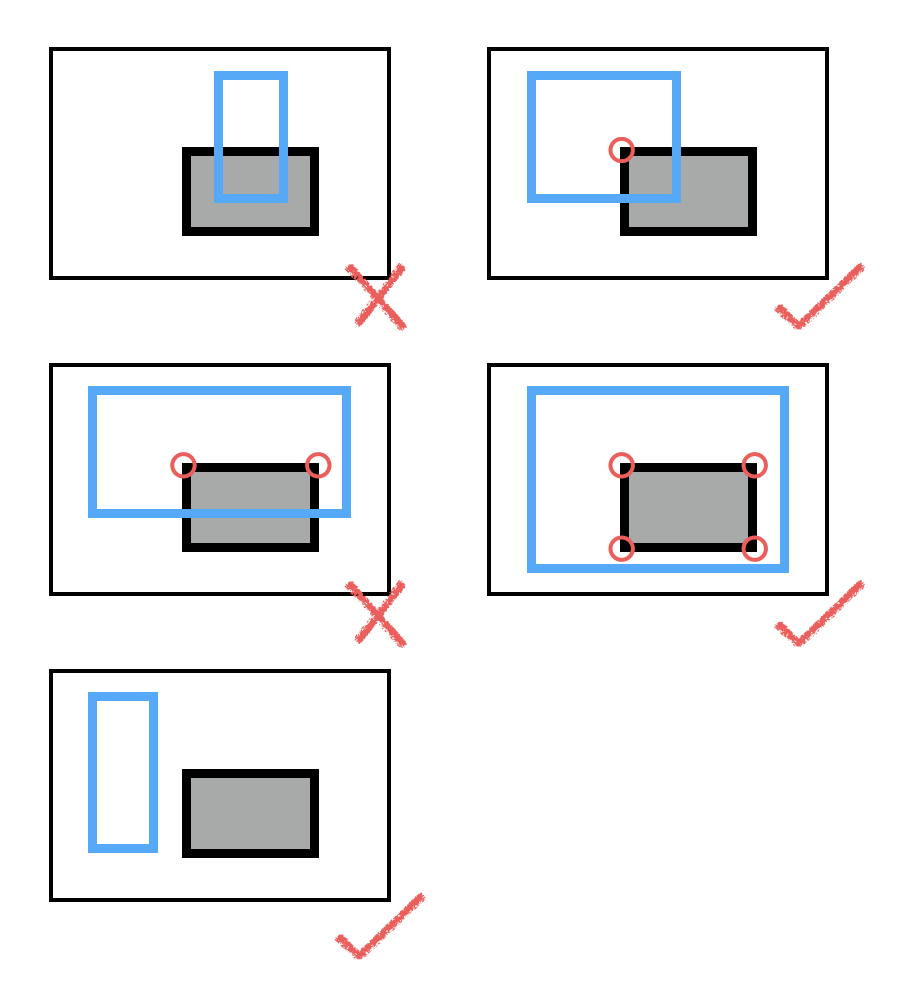
如果灰矩形在蓝矩形内部的顶点数分别对应了上面的几种情况。需要注意的是,顶点数为0实际上对应情况V和情况VI,但因为情况VI是非法的,所以这里需要额外判断一下。
代码:
1 #include <iostream> 2 3 using namespace std; 4 5 int n, m, L; 6 int l, r, t, b; 7 8 int run_horse(int pl, int pr, int pt, int pb) { 9 int ll = max(l, pl); 10 int rr = min(r, pr); 11 int tt = max(t, pt); 12 int bb = min(b, pb); 13 14 if (ll >= rr || tt >= bb) 15 return (pr - pl) * (pb - pt); 16 17 int inside = 0; 18 if (ll > pl && ll < pr && tt > pt && tt < pb) 19 inside++; 20 if (rr > pl && rr < pr && tt > pt && tt < pb) 21 inside++; 22 if (ll > pl && ll < pr && bb > pt && bb < pb) 23 inside++; 24 if (rr > pl && rr < pr && bb > pt && bb < pb) 25 inside++; 26 27 if (inside == 1 || inside == 4) 28 return (pr - pl) * (pb - pt) - (rr - ll) * (bb - tt); 29 else 30 return 0; 31 } 32 33 int main() { 34 int res = 0; 35 36 cin >> n >> m >> L; 37 cin >> l >> r >> t >> b; 38 39 for (int i = 0; i < n; i++) { 40 for (int j = 0; j < m; j++) { 41 int w = 1; 42 int h = (L - 2 * w) / 2; 43 while (w > 0 && h > 0) { 44 res = max(res, run_horse(j, min(m, j + w), i, min(n, i + h))); 45 w++; 46 h = (L - 2 * w) / 2; 47 } 48 } 49 } 50 51 cout << res << endl; 52 }