基础大概回顾
参考文献:Matlab GUI设计入门与实战
1.一维数据插值
interp1()函数,用于一维插值,其常用的插值方式如下:
1.1 nearest(最邻近插值)
在插值节点的近邻区域内取函数值,该插值函数是一个阶梯函数,即:
%% nearest
clc,clear,close all % 清理命令区、清理工作区、关闭显示图形
warning off % 消除警告
feature jit off % 加速代码运行
x = [1:10];
y = [1, 1, 7, 4, 0, 6, 3, 0, 8, 7];
figure('color',[1,1,1])
hold on
plot(x,y,'o--','linewidth',2) % 原数图形
xi = 1:0.1:10;
yi = interp1(x,y,xi,'nearest');
hold on
grid on
plot(xi,yi,'r*--','linewidth',2) % 原数图形
xlabel('x'); ylabel('y');
legend('原始数据','nearest插值')
1.2 linear(分段线性插值)
在每个小区间上采用简单的线性插值,在实际计算中,处理速度快,但是对海量数据本身以及非线性问题,处理误差大,线性插值获得的曲线不够平滑。
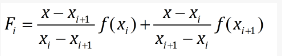
x = [1:10];
y = [1, 1, 7, 4, 0, 6, 3, 0, 8, 7];
xi = 1:0.1:10;
yi = interp1(x,y,xi);
1.3 spline(三次样条插值)
在每个分段内构造一个三次多项式,使其插值函数满足插值条件外,还要求每个节点处有光滑的条件(导数存在)。
x = [1:10];
y = [1, 1, 7, 4, 0, 6, 3, 0, 8, 7];
xi = 1:0.1:10;
yi = interp1(x,y,xi,'spline');
1.4 pchip(分段立方插值)
将插值的数据分段,针对每一段采用立方插值的方法进行拟合逼近
x = [1:10];
y = [1, 1, 7, 4, 0, 6, 3, 0, 8, 7];
xi = 1:0.1:10;
yi = interp1(x,y,xi,'pchip');
1.5 cubic(立方插值)
精度较高,插值曲线较平滑。
x = [1:10];
y = [1, 1, 7, 4, 0, 6, 3, 0, 8, 7];
xi = 1:0.1:10;
yi = interp1(x,y,xi,'cubic');
2.二维数据插值
griddata根据数据表[x,y,z],用不同的算法计算[xi,yi]各点上的函数近似值zi。
2.1 nearest(最近邻值)
x = [1:10];
y = [0, 0, 1, 1, 3, 4, 6, 7, 7, 8];
z = [8, 2, 8, 0, 3, 7, 8, 2, 4, 1];
Z = z'*ones(1,length(x));
xi = min(x):(max(x)-min(x))/50:max(x); % 插值数据
yi = min(y):(max(y)-min(y))/50:max(y); % 插值数据
yi = yi'; % 转置
Zi = griddata(x,y,Z,xi,yi,'nearest'); % 插值
mesh(xi,yi,Zi)
2.2 linear(线性插值)
Zi = griddata(x,y,Z,xi,yi,'linear'); % 插值
2.3 cubic插值
Zi = griddata(x,y,Z,xi,yi,'cubic'); % 插值
3.数据拟合
3.1 多项式最小二乘法
最小二次法拟合函数ployfit()
x = [1:10];
y = [8, 2, 8, 0, 3, 7, 8, 2, 4, 1];
p = polyfit(x,y,7); % 7次多项式
yc = p(1)*x.^7 + p(2)*x.^6+ p(3)*x.^5 + p(4)*x.^4 + p(5)*x.^3 + p(6)*x.^2 +...
p(7)*x.^1 + p(8)*x.^0;
3.2非线性拟合
函数lsqcurvefit()
4.选定区域处理
4.1 roicolor()函数
根据颜色选定区域,BW=roicolor(A,low,high),色图范围[low,high],返回这些像素选择区域。BW为内部值为1,外边为0的矩阵
obj=imread('ps.png');
obj=rgb2gray(obj);
load woman; % 加载MATALB自带图像对应的MAP值
BW=roicolor(obj,120,200); %抠图
figure,imshow(obj,map);
figure,imshow(BW);
4.2 roipoly函数
roipoly(I),为图像I生成交互式的处理界面;
roipoly(I,c,r),用向量c,r指定多边形的各点坐标。
obj=imread('psb.png');
r=obj(:,:,1);
g=obj(:,:,2);
b=obj(:,:,3);
c=[314 272 199 135 175 276]; %横坐标
r1=[163,268,276,171,43,32]; %纵坐标
BW=roipoly(obj,c,r1); %抠图
r1=immultiply(r,BW); %交运算
g1=immultiply(g,BW);
b1=immultiply(b,BW);
obj2=cat(3,r1,g1,b1); %合成RGB图像
subplot(121),imshow(obj);
subplot(122),imshow(obj2);