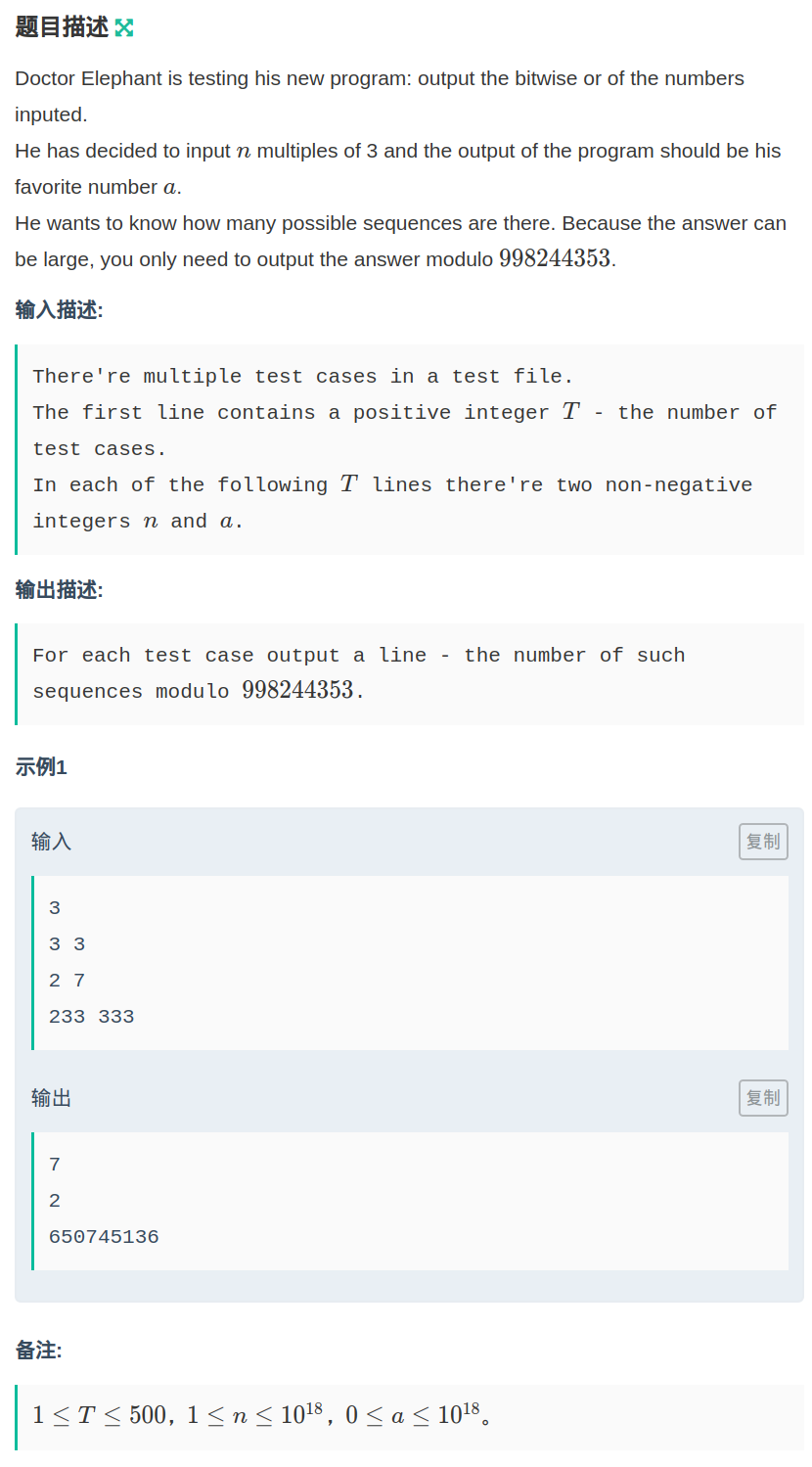
求用n个3的倍数的数按位或出数字a的方案数有多少种(0也算3的倍数)
题解
- 若数b的每个二进制位上的1,在a中也为1,则称b为a的子集
- 容易知道任意个a的子集按位或出来的结果还是a的子集
- 若问题改为按位或出来的结果是a的子集的方案数,那么答案就是a的子集中是3的倍数的子集个数的n次方
接着我们对子集按二进制上的1 mod 3的个数划分,例如1101有两个1mod3=1, 一个1mod3 = 2,设(S[i][j])表示a的子集中有i个mod3=1,j个mod3=2的子集的子集 中是3的倍数的个数,例如a = 1101的一个子集1001表示的状态为(S[1][1]), 1001的子集中是3的倍数的有1001和0000所以(S[1][1] = 2),那么(S[i][j])的n次方就可以表示为用n个3的倍数的数按位或出来的结果的状态是S[i][j]的子集方案数
那么(sum_{i=1}^kS[i][k-i])就表示或出来的结果最多匹配上a中K个1的方案数,那么我们就可以用最多匹配上a中K个1的方案数,减去匹配上a中K-1个1的方案数得出答案,但是这样简单的相减是不行的因为(S[i][k-i])的子集是会有重叠的,会多扣掉最多匹配k-2个1的方案数,根据容斥原理应当减去最多匹配K-1的方案数,加上最多匹配K-2的方案数,扣掉K-3加上K-4...
代码
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int mx = 65;
const ll mod = 998244353;
int C[mx][mx], S[mx][mx];
ll pow_mod(ll a, ll b) {
ll ans = 1;
while (b > 0) {
if (b & 1) ans = ans * a % mod;
a = a * a % mod;
b /= 2;
}
return ans;
}
int main() {
C[0][0] = 1;
for (int i = 1; i < mx; i++) {
C[i][0] = 1;
for (int j = 1; j <= i; j++) {
C[i][j] = (C[i-1][j-1] + C[i-1][j]) % mod;
}
}
for (int i = 0; i < mx; i++) {
for (int j = 0; j < mx; j++) {
for (int p = 0; p <= i; p++) {
for (int q = 0; q <= j; q++) {
if ((p + 2*q) % 3 != 0) continue;
S[i][j] += C[i][p] * C[j][q] % mod;
S[i][j] %= mod;
}
}
}
}
S[0][0] = 1;
int T;
scanf("%d", &T);
while (T--) {
ll n, a, x = 0, y = 0;
scanf("%lld%lld", &n, &a);
for (int i = 0; i < 64; i++) {
if (a & (1LL<<i)) {
if (i % 2 == 0) x++;
else y++;
}
}
ll ans = 0;
for (int i = 0; i <= x; i++) {
for (int j = 0; j <= y; j++) {
ll tmp = C[x][i] * C[y][j] % mod * pow_mod(S[i][j], n) % mod;
if ((x+y-i-j) % 2) tmp *= -1;
ans = (ans + tmp) % mod;
}
}
ans = (ans + mod) % mod;
printf("%lld
", ans);
}
return 0;
}