HDU2147 kiki's game

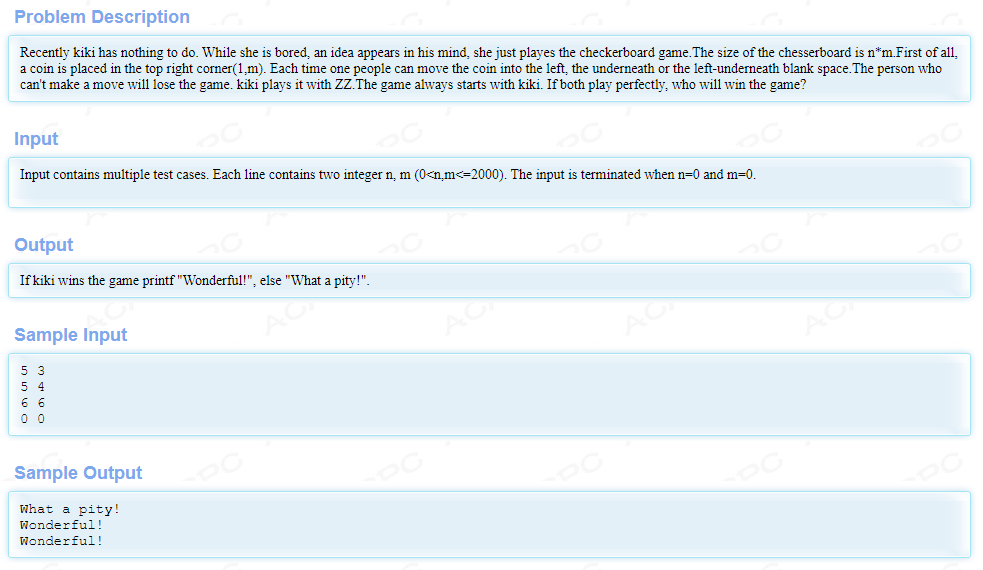
题面

    
找规律的方法耗时比较久，我们来说说如何用SG函数的方法。

前置知识

1. 首先考虑此游戏是一个什么游戏，先来看看有向图游戏定义
   给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。该游戏被称为有向图游戏。
   很显然，本题属于有向图游戏（网格图可以看作有向无环图）。
   有向图游戏先手必胜，当且仅当有向图游戏的起点(s)的SG函数值不为(0)。
2. 什么是SG函数？
   先来介绍(mex)运算，设(S)表示一个非负整数集合。定义(mex(S))为求出不属于集合(S)的最小非负整数的运算，即：

[mex(S) = min_{xin N,x otin s}{{x}} ]

举个栗子，如果集合(S)里有({2，4，5})，那么经过(mex)运算后的值为(0)。
       定义(SG(x))为(x)的后继节点(y_1,y_2,cdots,y_k)的(SG)函数值构成的集合再执行(mex)运算的结果，即：

[SG(x) = mex({SG(y_1),SG(y_2),cdots,SG(y_k)}) ]

特别的，整个有向图游戏(G)的SG函数值被定义为起点的(SG)函数值。
SG函数还有一个性质，有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于零。
回到这个题目上就是要保证起点的SG函数值不为零。（因为kiki先走）
3. 问题转化为求该网格图的SG函数值，那么终点的SG函数值一定为(0)，递推即可求出答案。
但是，题目给的空间有限，开(2000*2000)的int可能不够。考虑优化，现给出(4*4)网格图的SG函数值：
                                                              
可以发现，为(0)都是必输局面，大于(0)的都是必胜局面,emmmmm，等下，大于(0)，也就是我们不需要知道具体的SG函数值是多少，只要他大于零，就是必胜局面。那我们可以换成(1)。
所以我们只需开一个二维bool数组来记录每一点的必胜情况即可。

代码

#include<bits/stdc++.h>
using namespace std;
bool a[2001][2001];
int main()
{
	int n,m;
	a[1][1] = 0;
	for(int i = 2;i <= 2000;i ++ )
	{
		a[i][1] = !a[i-1][1];
	}
	for(int i = 2;i <= 2000;i ++ )
	{
		a[1][i] = !a[1][i-1];
	}
	for(int i = 2;i <= 2000;i ++ )
	{
		for(int j = 2;j <= 2000;j ++ )
		{
			if(a[i-1][j] && a[i-1][j-1] && a[i][j-1])
			{
				a[i][j] = 0;
			}
			else a[i][j] = 1;
		}
	}
	
	while(cin >> n >> m)
	{
		if(n == 0 && m == 0) break;
		if(a[n][m]) cout << "Wonderful!" << endl;
		else cout << "What a pity!" << endl;
	}
	return 0;
}

后记

这道题摸了好久，可算是摸出来了。