公交车问题
问题描述
一条线路上有 n 个公交车站,假设在到达第 i 个站点之前,车上总共有 x 个乘客,过了该站点后车上总共有 y 个乘客,
司机会把 y-x 这个数字,即乘客数量变化值 d_i 记录下来,公交车有固定的载客量 g,若有一份司机的开车日志,车上乘客数量的可能情况有多少种
输入输出
输入: 第一行有两个数字 n 和 g,分别表示站点数量及当前撤了的最大载客数量(1 <= n,g <= 1000)
第二行共 n 个数字,由空格分开,经过第 i 个公交车站后车上乘客的变化数量 d_i (-1000 <= d_i <= 1000)
输入数据保证从总站出发时乘客数量大于等于 0
输出:输出一个数字,即司机从总站出发时,车上乘客数量的可能性个数。
样例
// 样例输入一:
4 10
1 2 3 4
// 样例输出一:
1
// 样例输入二:
4 5
2 -1 2 1
// 样例输出二:
2
问题分析
绘出示意图
按照题中信息,可以画出如下的示意图:
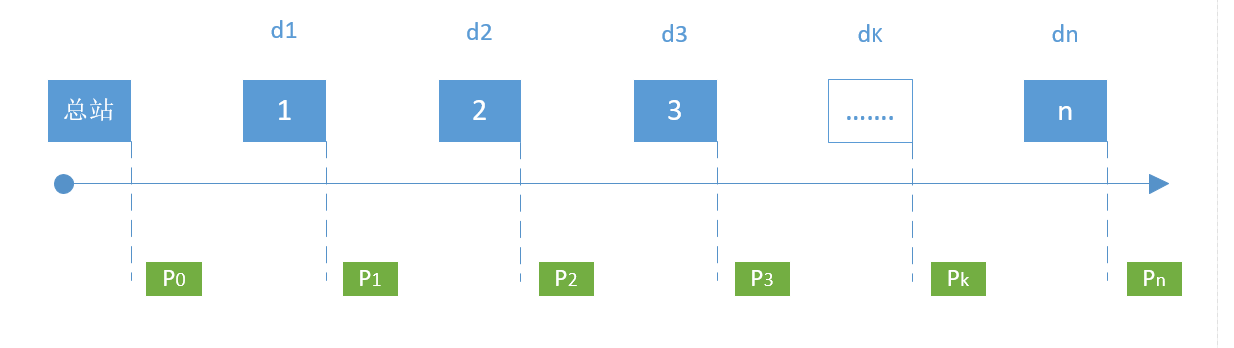
其中蓝色方框表示各个站点, di 即是第 i 站点的乘客数量变化,Pi 是经过第 i 个站点后车上的乘客数量。
可以得到等式:
- Pi - Pi-1 = di ,其中 0 < i <= n
数学推导
由于公交车的载客量为 g,那么对于每个 Pi 而言,都会存在默认的约束条件 0 < Pi < g。
简单情况:
考虑等式:P1 - P0 = d1:
对于减数 P0 而言,它的取值范围在
- [P1min-d1, P1max-d1],
由默认的约束条件得到取值范围:
- [0, g-d1],
实际上这个范围成立的条件是 d1 >= 0,而实际上 d1 可以取负值,所以 P0 的取值范围应该修正为
- [max(0, -d1), min(g-d1, g)];
对于被减数 P1 而言,同样可以得到其取值范围在
- [max[0, d1], min(g+d1, g)]`。
推广到一般情况:
对于所有作为减数的 Pj (0 <= j < n),它的取值范围是
- [max(0, -dj+1), min(g-dj+1, g)];
而对于所有作为被减数的 Pk (0 < k <= n),它的取值范围是
- [max(0, dk), min(g+dk, g)]。
Pi-1 取最大范围 [0, g]
在第 1 站到终点站之间的 Pi,即可以与 Pi-1 关联的等式中作为被减数,又可以与 Pi+1 关联的等式作为减数,因此是可以得到两个取值范围的,取其交集,得 Pi (0 < i < n)的范围是
- [max(0, -di+1, di), min(g, g-di+1,, g+di)];
特殊的如 P0 范围:[max(0, -d1), min(g-d1, g)]; 或 Pn 范围:[max(0, dn), min(g+dn, g)]。
从 P0 的范围开始迭代计算
然而以上利用 Pi-Pi-1=di 对 Pi 范围进行的推导是建立在把 Pi-1 的取值范围当作静态的 [0, g] 而得出的 Pi 范围,实际上 Pi-1 的范围可能比静态的 [0, g] 要小。
若已经求得 Pi-1 的范围是 [R1, R2] (0 <= R1 <= R2 <= g),那么作为被减数的 Pi 的取值范围应为:
- [R1+di, R2+di]
与上面得到的 Pi 的取值范围取交集,得到:
- [max(0, R1+di, -di+1), min(g, R2+di, g-di+1)]
由于 P0 的范围是确定的 [max(0, -d1), min(g-d1, g)],因此通过上式可以递归算出 Pi 的取值范围。
结果推导
通过数学分析推导,若得出 Pi 的范围为 [RiMin, RiMax],那么第 i 个站点后的人数可能情况就为
RiMax - RiMin + 1
取这些情况中值最小的那个,就是公交车经过整条路线时的人数变化的可能情况,也就是从总站出发时的人数可能情况。
主要代码
推导出数学公式后,编写代码就非常容易了。主要代码如下:
int tmpMax = carSize, tmpMin = 0;
// 算出 P0 的最小最大值
person[0*2] = getMax(0, -diff[0]);
person[0*2+1] = getMin(carSize, carSize - diff[0]);
// 迭代算出 P1 - Pn-1 的最小最大值
for(int i = 1; i < station; i++) {
tmpMin = person[(i-1)*2];
tmpMax = person[(i-1)*2+1];
person[i*2] = getMax( 0, tmpMin + diff[i-1], -diff[i] );
person[i*2+1] = getMin( carSize, tmpMax + diff[i-1], carSize - diff[i] );
}
// 算出 Pn 的最小最大值
tmpMin = person[(station-1)*2];
tmpMax = person[(station-1)*2+1];
person[station*2] = tmpMin + diff[station-1];
person[station*2+1] = tmpMax + diff[station-1];
这段代码用到的最大最小值的求值公式就是由上述数学推导而来。
其它的解法
上述数学推导用到的方法是迭代求取范围,最开始思考这个题的时候的思路是假设 Pi-1 都取最大范围 [0, g],使用以下公式:
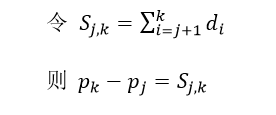
遍历所有可能去到的 k 和 j,利用 Pj 的范围求出 Pk 的范围,相应的代码虽然能够解出,但是并不好理解,执行效率比前面所说的迭代方法低。以下是之前版本代码的主要部分:
int tmp = 0, tmpMax = carSize, tmpMin = 0;
tmp = carSize - d_i[0];
if( tmp < carSize ) {
person[1] = tmp;
}
for(int gap = 1; gap < station; gap++) {
for(int i = gap; i < station + 1; i++) {
tmpMax = person[(i-gap)*2+1] + personChanged(i-gap, i);
tmpMin = person[(i-gap)*2] + personChanged(i-gap, i);
if( i < station) {
// 最后一个计算的时候没有额外的约束条件了
tmp = carSize - d_i[i];
tmpMax = getMin(tmp, tmpMax); // 取较小的(即取交集)
}
if( tmpMax < tmpMin ) {
// 若上限小于下限,对应的不等式不成立,说明不存在这种情况
cases = 0;
return;
}
tmpMax = getMin(tmpMax, carSize);
person[i*2+1] = getMin(person[i*2+1], tmpMax);
tmpMin = getMax(0, tmpMin);
person[i*2] = getMax(person[i*2], tmpMin);
}
}
总结
这个问题其实比较简答,思考的时候需要紧紧抓住 Pi 的定位,即它到底是作为减数还是被减数来求得范围的,否则就容易陷入思维误区,无法快速得到计算范围的公式。