软件工程实践2019第三次作业

2019.9.25 21:27更新：优化了命令行参数的读取，在交作业前vs正式的单元测试可能来不及了

准备

Github地址

https://github.com/Brokenpumpkin/031702543

PSP表格

PSP2.1	Personal Software Process Stages	预估耗时(min)	实际耗时(min)
Planning	计划	30	30
Estimate	估计这个任务需要多少时间	30	30
Development	开发	2260	1665
Analysis	需求分析（包括学习新技术）	360	300
Desgin Spec	生成设计文档	30	10
Design Review	设计复审	10	5
Coding Standard	代码规范（为目前的开发制定合适的规范）	60	30
Design	具体设计	120	60
Coding	具体编码	900	900
Code Review	代码复审	480	120
Test	测试（自我测试，修改代码，提交修改）	300	240
Reporting	报告	270	220
Test Repor	测试报告	180	180
Size Measurement	计算工作量	20	10
Postmortem & Process Improvement Plan	事后总结，并提出过程改进计划	60	30
合计		2560	1915

解题

1.思考

百度百科：数独盘面是个九宫，每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次，所以又称“九宫格”。

任务：完成从三宫格到九宫格的进阶

刚开始看题目的时候，因为题目说完成三宫格就给基本分，有点被误导，想从三宫格推到九宫格，转头想了想其实从九宫格推到三宫格更简单，我们可以将n宫格，分为需要划分和不需要划分，需要划分的通过n宫格划分的特性将里面的宫的长宽的长度设为两个变量，就可以对宫进行操作。我是用递归的方法进行解题的，在解比较难的数独时可能时间会比较长一点。

2.唯一性函数

首先要判定数字i在（x，y）时，i在x行，在y列（有宫时在所在的宫内）是否是唯一的。在数独中，同一行、同一列、同一宫中不能出现相同的数字，如果找到相同的就返回false。

bool check(int x,int y,int i) //判断在(x,y)处数字i在同一行、列、宫是否唯一
{
	int l, w;
	for (l = 0; l < gsiz; l++) //按列检查同一行是否有重复
	{
		if (l != y&&single_bor[x][l] == i)
			return false;
	}
	for (w = 0; w < gsiz; w++)//按行检查同一列是否有重复
	{
		if (w != x&&single_bor[w][y] == i)
			return false;
	}
	if (glen != gsiz) //如果有宫
	{
		for (l = (x / glen)*glen; l < (x /glen)*glen +glen; l++) 
		{
			for (w = (y /gwid)*gwid; w < (y /gwid)*gwid +gwid; w++)
			{
				if (single_bor[l][w] == i)
				{
					if (l == x&&w == y)
						continue;
					else
						return false;
				}
			}
		}
	}
	return true;
}

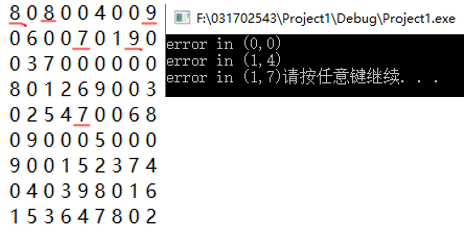
测试check函数我是在input.txt文件中添加行相同，列相同，宫相同的例子，然后在主函数中调用check函数，如果发现有错便输出。

测试代码：

if (!check(0, 0, 8))//行
	cout << "error in (0,0)" << endl;
if (!check(1, 4, 7))//列
	cout << "error in (1,4)" << endl;
if (!check(1, 7, 9))//宫
	cout << "error in (1,7)";

3.探求函数

解决完唯一性函数后，我们再来真正的解决数独问题。我一开始是没有想到用递归的，后来在看了网上各位大佬的思路才了解到可以运用递归。其实运用递归就是一个暴力解数独的过程，相当于一个穷举，在现实中肯定没有人会用这种方法解数独。DSF函数要先通过x = depth / gsiz, y = depth % gsiz，求出（x，y），然后如果该位置上已经有数字，就调用DSF（depth+1)函数，进入下一格，如果该位置上没有数字就将1~gsiz（gsiz是宫的大小）的数字填入一个，此时检查该数字的唯一性，若不唯一就填入下一个数字，直到有数字具有唯一性则调用DSF（depth+1）函数，进入下一格。若某一格所有数字试完都不满足唯一性，则将它继续置0，返回上一个depth。所以如果一个数独无解，调用这个函数输出的会是原来输入的数独。

bool DSF(int depth) //利用递归分别探求每个格子填入哪个数字
{
	int i, x, y;
	if (depth >= gsiz*gsiz)
		return true;
	x = depth / gsiz, y = depth % gsiz;
	if (single_bor[x][y] != 0)//（x,y)已赋值
		return DSF(depth + 1);
	else
	{
		for (i = 1; i <= gsiz; i++)
		{		
			if (check(x, y, i))
			{
				single_bor[x][y] = i;	
				//cout << i << "填入" << depth << "
"; 
				if (DSF(depth + 1))
					return true;
			}
			single_bor[x][y] = 0;
		}	
	}
	return false;
}

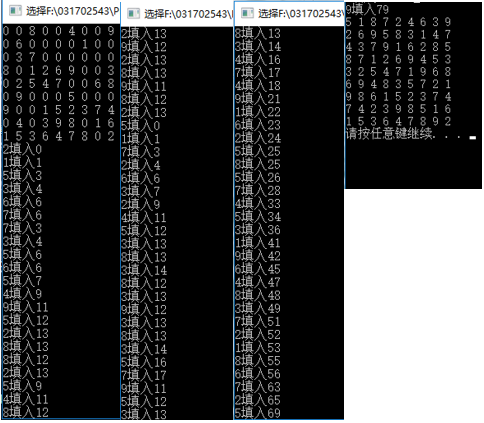
测试DSF函数的方法，我是在该函数中加了cout << i << "填入" << depth << " "语句，这样主函数每次调用DSF函数时都会输出一行文字，然后只需观察depth的值就行了。再将主函数中改成相应部分改成以下代码：

for (i = 0; i < num; i++)
{
	for (j = 0; j < gsiz; j++)
	{
		for (k = 0; k < gsiz; k++)
		{
			cout << single_bor[j][k];
			if (k != gsiz - 1)
				cout << " ";
		}
		if (j != gsiz - 1)
			cout << "
";
	}
	if (i != num - 1)
		cout << "

";
}
cout << endl;
DSF(0);
for (i = 0; i < num; i++)
{
	for (j = 0; j < gsiz; j++)
	{
		for (k = 0; k < gsiz; k++)
		{
			cout << single_bor[j][k];
			if (k != gsiz - 1)
				cout << " ";
		}
		if (j != gsiz - 1)
			cout << "
";
	}
	if (i != num - 1)
		cout << "

";
}

单一九宫格测试样例：

4.主函数

命令行传参输入后传入的是一个二维数组，数好二维数组行的序号可以把二维数组的一行直接拿出来用。

本来文件输入输出我打算用fstream头文件解决的，但我一开始测试了一下发现如果用ifstream读文件读进来是读字符串进来，连空格都会读，然后我疯狂的百度有没有什么解决办法，最后要感谢先交作业的几位大佬，我发现他们都用的FILE类，就去查了下用法拿来用了，FILE类可以直接读数字，让我工作量减轻了不少。

主函数一开始读入n宫格的大小后，通过n宫格的特性，将3/6/9宫格分为一类，4/8宫格分为一类，5/7宫格分为一类。

int main(int argc,char *argv[])
{
	int  i, j, k;
	int InputFile=0, OutputFile=0;
	string m = "-m",in = "-i", out = "-o",  n = "-n";
	if (argc > 0 && argv != NULL)
	{
		for (i = 0; i < argc; i++)
		{
			
			if (argv[i] == in)
				InputFile = i + 1;
			if (argv[i] == out)
				OutputFile = i + 1;
			if(argv[i]==m)
				gsiz = atoi(argv[i + 1]);
			if(argv[i]==n)
				num = atoi(argv[i + 1]);
		}
	}
	else
	{
		cout << "未输入参数" << endl;
	}
		
	FILE* afile;
	afile = fopen(argv[6], "r");
	if (afile == NULL)
	{
		cout << "cannot find input file" << endl;
		return 0;
	}
	for (i = 0; i < num; i++)
	{
		for(j = 0; j < gsiz; j++)
			for(k = 0;  k< gsiz; k++)
				fscanf(afile, "%d", &single_bor[j][k]);
		DSF(0);
		for (j = 0; j < gsiz; j++)
			for (k = 0; k < gsiz; k++)
				out_bor[i][j][k] = single_bor[j][k];
	}
	fclose(afile);
	
	afile = fopen(argv[8], "w");
	for (i = 0; i < num; i++)
	{
		for (j = 0; j < gsiz; j++)
		{
			for (k = 0; k < gsiz; k++)
			{
				fprintf(afile, "%d", out_bor[i][j][k]);
				if (k != gsiz - 1)				
					fprintf(afile, " ");			
			}
			if (j != gsiz - 1)			
				fprintf(afile, "
");		
		}
		if (i != num - 1)	
			fprintf(afile, "

");
					
	}
	fclose(afile);
    return 0;
}

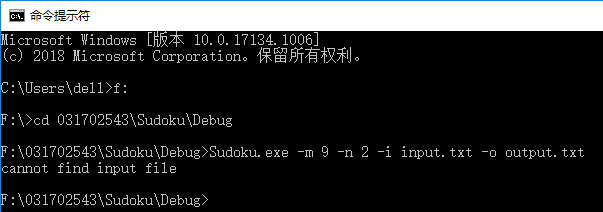
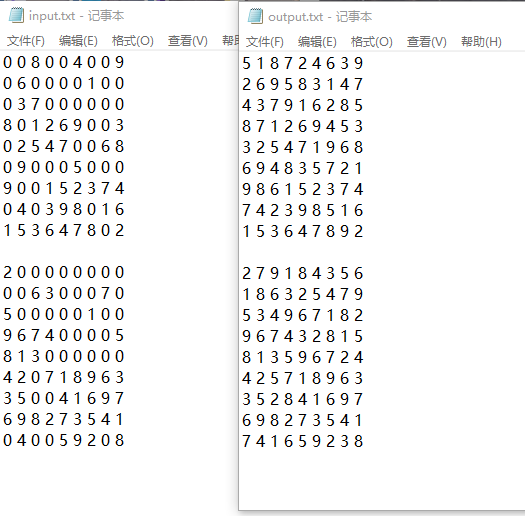
当找不到相应的输入文件时：

测试

1.Code Quality Analysis工具分析

2.性能分析

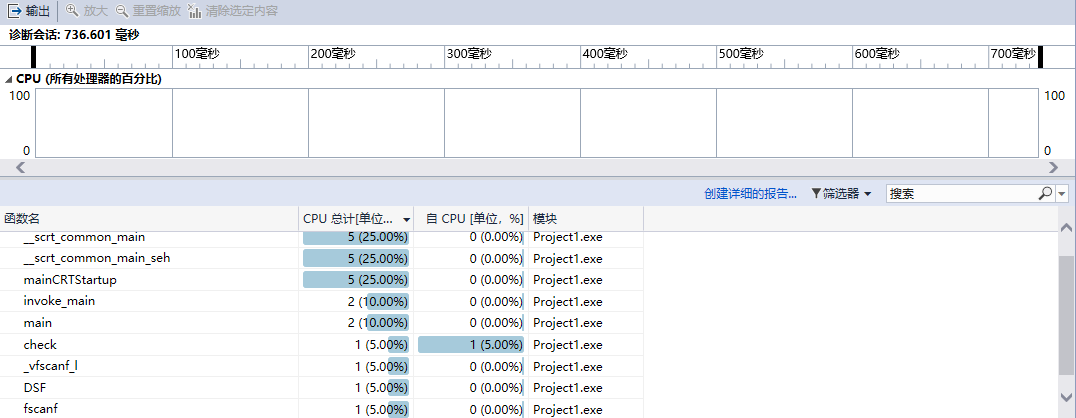
额。。因为不知道加了命令行要怎么进行性能分析，所以我新建了个项目删去了命令行有关的东西，利用作业博客中的样例直接将宫的大小设置为9，盘面为2，进行性能分析。

九宫格样例性能分析：

3.样例测试

三宫格与四宫格：

五宫格与六宫格：

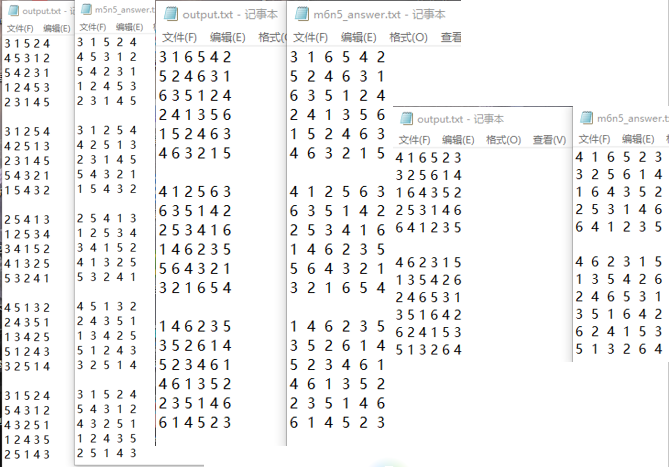
七宫格

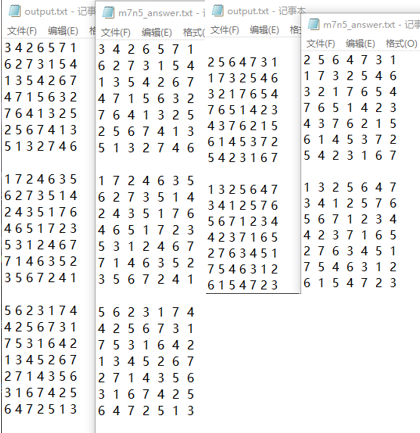
八宫格：

九宫格：

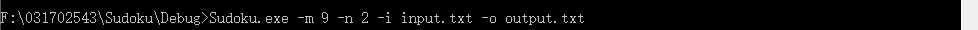
总结

该项作业一路走来，解决了很多之前一窍不通的地方，比如文件输入输出，命令行传参，Visual Studio的基本使用，也回顾了一下以前的知识，如递归调用。但还是有一些不足的地方，例如vs的c++程序用到命令行传参时，一开始不懂得性能向导里可以输入命令行参数，性能探查器会停止运行，之后在性能向导里输入命令行参数后，结果发现性能分析文件是空的，至今我只想到新建一个项目，将参数在main函数内定好去性能分析，还有就是代码的优化，我在网上有看到Dance Links算法，但是要用到矩阵而且我看得不是很懂就又回归到递归的怀抱了，写完这个版本的代码后就不怎么敢推倒重来了。（感觉有点知难而退的意思。。。）