1. 复杂信号的组成

简单信号的产生

2. 频域的概念
从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。
在你的理解中,一段音乐是什么呢?

这是我们对音乐最普遍的理解,一个随着时间变化的震动。但我相信对于乐器小能手们来说,音乐更直观的理解是这样的:

是的,其实这一段写到这里已经可以结束了。上图是音乐在时域的样子,而下图则是音乐在频域的样子。所以频域这一概念对大家都从不陌生,只是从来没意识到而已。
现在我们可以回过头来重新看看一开始那句痴人说梦般的话:世界是永恒的。
将以上两图简化:
时域:

频域:

你眼中看似落叶纷飞变化无常的世界,实际只是躺在上帝怀中一份早已谱好的乐章。
(众人:鸡汤滚出知乎!)
抱歉,这不是一句鸡汤文,而是黑板上确凿的公式:傅里叶同学告诉我们,任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加。在第一个例子里我们可以理解为,利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲。
而贯穿时域与频域的方法之一,就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation),我们从简单的开始谈起。
3. 傅里叶级数 (Fourier Series)
如果我说我能用前面说的正弦曲线波叠加出一个带 90 度角的矩形波来,你会相信吗?你不会,就像当年的我一样。但是看看下图:

- 第一幅图是一个郁闷的正弦波 cos(x)
- 第二幅图是 2 个卖萌的正弦波的叠加 cos(x)+a.cos(3x)
- 第三幅图是 4 个发春的正弦波的叠加
- 第四幅图是 10 个便秘的正弦波的叠加
随着正弦波数量逐渐的增长,他们最终会叠加成一个标准的矩形,大家从中体会到了什么道理?(只要努力,弯的都能掰直!)
随着叠加的递增,所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个正弦波叠加起来才能形成一个标准 90 度角的矩形波呢?不幸的告诉大家,答案是无穷多个。
不仅仅是矩形,你能想到的任何波形都是可以如此方法用正弦波叠加起来的。这是没有接触过傅里叶分析的人在直觉上的第一个难点,但是一旦接受了这样的设定,游戏就开始有意思起来了。
还是上图的正弦波累加成矩形波,我们换一个角度来看看:
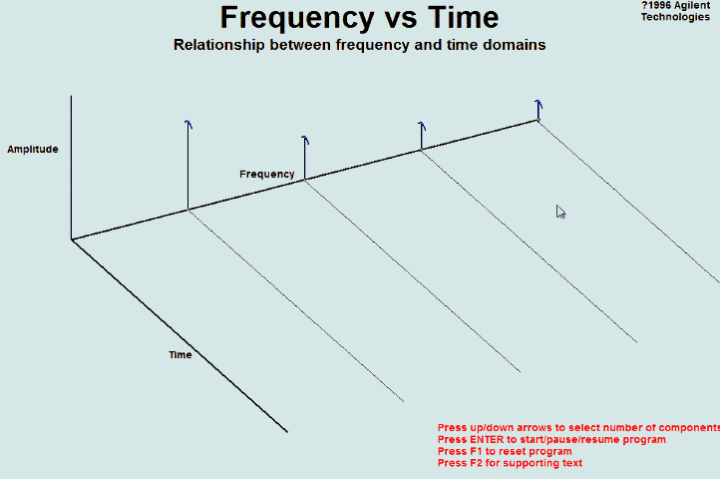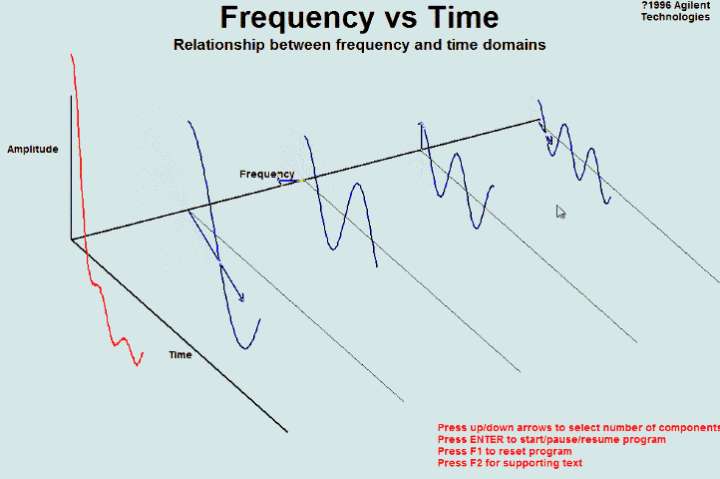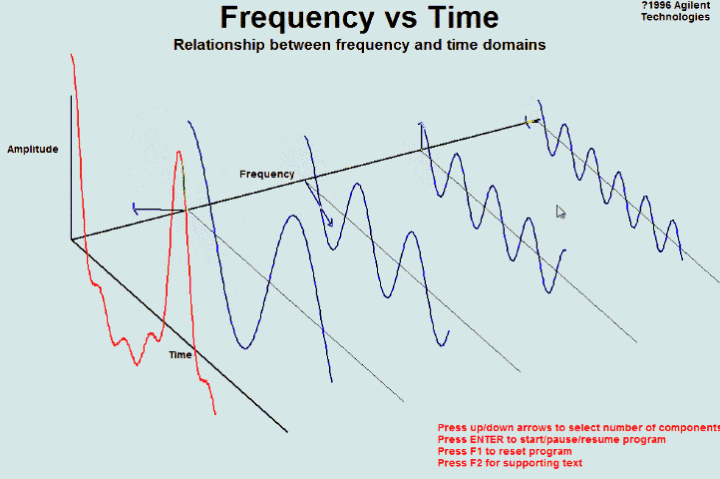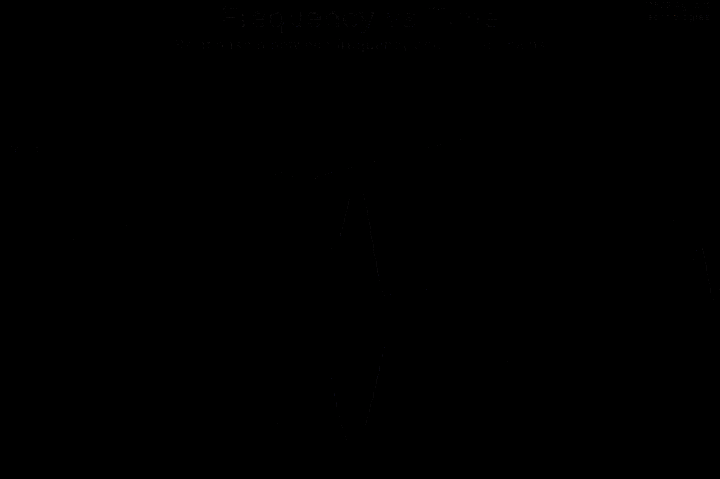
这里,不同频率的正弦波我们成为频率分量。
如果我们把第一个频率最低的频率分量看作 “1”,我们就有了构建频域的最基本单元。
对于我们最常见的有理数轴,数字 “1” 就是有理数轴的基本单元。(好吧,数学称法为——基。在那个年代,这个字还没有其他奇怪的解释,后面还有正交基这样的词汇我会说吗?)
时域的基本单元就是 “1秒”,如果我们将一个角频率为 ω 的正弦波 cos(ωt) 看作基础,那么频域的基本单元就是 ω 。

有了 “1”,还要有“0” 才能构成世界,那么频域的 “0” 是什么呢? cos(0t) 就是一个周期无限长的正弦波,也就是一条直线!所以在频域,0 频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。
正弦波就是一个圆周运动在一条直线上的投影。所以频域的基本单元也可以理解为一个始终在旋转的圆
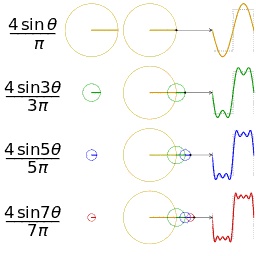
再清楚一点:

可以发现,在频谱中,偶数项的振幅都是 0,也就对应了图中的彩色直线。振幅为 0 的正弦波。
4. 傅里叶变换
信号,比如生活中一个声音信号,整个波形是混乱看不出规律的。但是傅立叶就说,其实一个信号再怎么乱,也不过是由简单波形的组合而来的,比如正弦波。高频率,低频率的正弦波,按不同比例调配起来能得到你最终要的那个混乱不堪的声音信号(就是这么神奇)。声音信号千千万,只是取决于比例有千千万。
这个信号混乱不堪,但是傅立叶说,其实可以用一个方法,分析出这个信号各个频率的比例是多少的。
——傅立叶变换,就是这个方法了。
常用的傅里叶变换是把信号从时间/幅度平面转换到频率/幅度平面,另外还有一类分析方法时将其转换到时间/频率平面,称为时频分析,也可利用傅里叶变换的一种变形方法完成。
5. 行业应用
5.1. 频率提取
比如,我检测到一个信号是这样的:
m=cos(x)+cos(10*x)+cos(50*x)+cos(100*x)+cos(500*x)+cos(1000*x);
这个信号里面包含了六个不同频率的正弦波信号。那它看起来是怎样的呢?
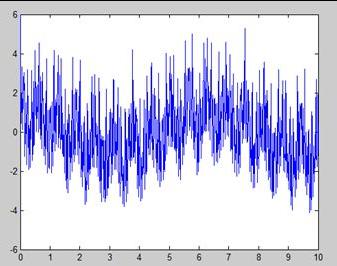
看到这样的一个图,你有信心从里面提取出什么关键的信息吗?面对这种一团乱麻的波形图,我们的内心是崩溃的。然而,现在对它做一下快速傅里叶变换,就得到这样的频域图像:

很明显就能看到,以pi轴为对称轴(关于傅里叶变换的对称性在这里就不多展开了),pi轴左边和右边分别有六个峰,完美的对应原函数里面六个不同的正弦频率组合。这种提取在地震波信号分析、音频处理等等常常是很好用的。
5.2. 降噪
比如你在录音,麦克风质量不大好,始终有个固定的高频电流声(吱吱吱),于是最终的音频文件记录下来的信号就是你的声音跟电流声混在一起的那么一个信号。这个时候你就可以在电脑上用傅立叶来分析看看,过滤掉频率过高的不可能是人发出的,然后提取出纯粹的人声。
数字图片中,一个颜色有一个值,比如红色跟蓝色就是用不同值表示。你拍了一张蓝天的照片,画面基本就是蓝的,但相机不大好,出现噪点,噪点是红色的。把这张照片的像素从左到右从上到下一个个,类似柱状图那样把颜色值表示出来,就变成了一个信号波形(Photoshop 有提供这功能),波形总体就是平缓的一个波形,因为都是差不多的颜色,颜色值差不远。但就是有一个尖峰,尖峰其实就是那个红色噪点。一个信号会出现尖峰,说明这个地方混入了高频率信号。这时傅立叶分离高低频率的能力就可以拿来图片降噪了。
5.3. 去燥
有时候,我们需要对一个信号进行检测,但是实际检测的过程中会出现各种各样的干扰(静电干扰,噪声干扰等等)。假设我们需要检测的原始信号是这样的:

但是这个信号受到了这样一个高频噪声的干扰:
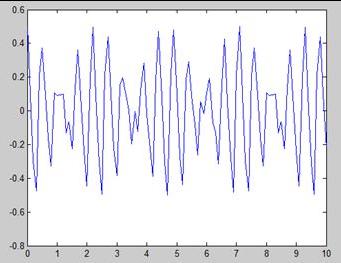
所以我们最后只能检测到这样的信号:

然而有了傅里叶变换,我们不会轻易的狗带。对检测到的信号做一下傅里叶变换,得到:

假设我们已经知道需要检测的信号是比较低频的,而干扰噪声是高频的。那么对得到的频域信号进行低通滤波处理,得到:

也就是说我就只要低频的信号,删掉高频的信号。对这个信号进行傅里叶反变换,得到:
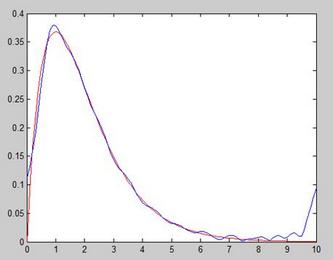
可以看到通过傅里叶变换和反变换,从一个完全杂乱无章的信号里面,提取出了我们期望的低频信号,而滤掉了高频信号。
之前
@凌晨晓骥所提到的是图像去噪,属于二维空间信号去噪,而在理论上傅里叶变换可以用于任意维度的时域或空间域信号的去噪,当然,实际应用中常见的还是一维和二维。其原理在于:信号中的有效成分(可认为是目标)和噪声的频率往往是不同的,在经过傅里叶变换之后,噪声和目标分量在频域上分别位于不同的频率中,便于将其进行区分。
5.4. 边缘提取
在图像处理中还有一个很重要的题目就是边缘提取,也可以利用傅里叶变换完成,这是由于边缘区域的色彩变化通常较大,频率较高,而非边缘区域色彩变化平缓,频率较低。
5.5. 滤波
显而易见,只要信号的频率不同,就可以分解出来。
实际上,任何对于信号的操作都属于滤波,而只要是滤波就可以利用傅里叶变换实现。
但是!(不错,最后总是会有一个但是!),傅里叶变换只是理论上的最优,它需要无限的信号长度才能准确的得到其中各个分量的频率,而在实际应用中,信号的长度始终是有限的,所以需要使用其他针对有限长度信号的变换方式对其频域进行提取。另一方面,由于目前大部分信号处理都是通过数字信号完成的,受到采样频率和奈奎斯特采样定律的限制,不可能得到信号所有的频率分量。
6. 快速傅里叶变换(Fast Fourier Transform, FFT)
离散傅里叶变换(Discrete Fourier Transform, DFT)是数字信号处理最重要的基石之一,也是对信号进行分析和处理时最常用的工具之一。在200多年前法国数学家、物理学家傅里叶提出后来以他名字命名的傅里叶级数之后,用DFT这个工具来分析信号就已经为人们所知。但在很长时间内,这种分析方法并没有引起更多的重视,最主要的原因在于这种方法运算量比较大。
快速傅里叶变换(Fast Fourier Transform, FFT)是1965年由库利(T.W.Cooley)和图基(J.W.Tukey)共同提出的一种快速计算DFT的方法。这种方法充分利用了DFT运算中的对称性和周期性,从而将DFT运算量从N2减少到 N*log2N 。当N比较小时,FFT优势并不明显。但当N大于32开始,点数越大,FFT对运算量的改善越明显。比如当N为1024时,FFT的运算效率比DFT提高了100倍。
在库利和图基提出的FFT算法中,其基本原理是先将一个N点时域序列的DFT分解为N个1点序列的DFT,然后将这样计算出来的N个1点序列DFT的结果进行组合,得到最初的N点时域序列的DFT值。实际上,这种基本的思想很早就由德国伟大的数学家高斯提出过,只是由于当时尚欠东风——计算机还没发明。在20世纪60年代,伴随着计算机的发展和成熟,库利和图基的成果掀起了数字信号处理的革命,因而FFT发明者的桂冠才落在他们头上。
7. 理解变换
类比:向量可以通过代数来表示,代数A(2,1)也可以还原(逆变换)为向量。
时域信号,通过傅立叶变换,输出为:
- 一系列的频率
- 每个频率下的振幅
- 每个频率的相位
7.1. 傅里叶变换的分类
模拟信号:
-
(连续)傅里叶级数(Fourier Series,CFS)
实现了时域与频率的变换过程。
但是!它只能处理周期性函数,适用于连续周期信号。而现实中的信号,多是无周期的函数:
-
(连续)傅立叶变换(Fourier Transform,FT)
比如衰减指数曲线和高斯曲线。
但是,计算机只能处理数字信号,首先需要将原模拟信号在时域离散化:
- 离散时间傅立叶变换(Discrete Time Fourier Transform,DTFT)
注意:此时时域是离散的,而频域依然是连续的。
经过上面两个步骤,我们得到的信号依然不能被计算机处理,因为频域既连续,又周期。我们自然就想到,既然时域可以采样,为什么频域不能采样呢?这样不就时域与频域都离散化了吗?没错,接下来对频域在进行采样。
-
离散傅立叶变换(Discrete Fourier Transform,DFT)
用于处理离散周期信号,也是最早的研究方向。
FFT呢?FFT的提出完全是为了快速计算DFT而已,它的本质就是DFT!我们常用的信号处理软件MATLAB或者DSP软件包中,包含的算法都是FFT而非DFT。
对于离散序列的z变换,如果将z用exp(j*数字角频) 做变量替换,则z变换退化为DTFT。