图文详解两种算法：深度优先遍历（DFS）和广度优先遍历（BFS）

参考网址：图文详解两种算法：深度优先遍历（DFS）和广度优先遍历（BFS） - 51CTO.COM

深度优先遍历(Depth First Search, 简称 DFS) 与广度优先遍历(Breath First Search)是图论中两种非常重要的算法，生产上广泛用于拓扑排序，寻路(走迷宫)，搜索引擎，爬虫等，也频繁出现在 leetcode，高频面试题中。

本文将会从以下几个方面来讲述深度优先遍历，广度优先遍历，相信大家看了肯定会有收获。

• 深度优先遍历，广度优先遍历简介
• 习题演练
• DFS，BFS 在搜索引擎中的应用

深度优先遍历，广度优先遍历简介

深度优先遍历

主要思路是从图中一个未访问的顶点 V 开始，沿着一条路一直走到底，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底...，不断递归重复此过程，直到所有的顶点都遍历完成，它的特点是不撞南墙不回头，先走完一条路，再换一条路继续走。

树是图的一种特例(连通无环的图就是树)，接下来我们来看看树用深度优先遍历该怎么遍历。

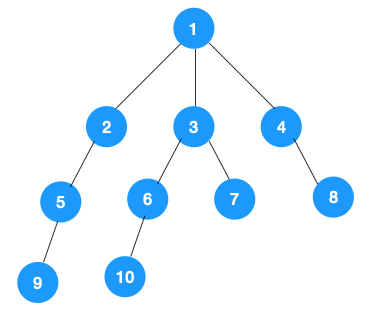
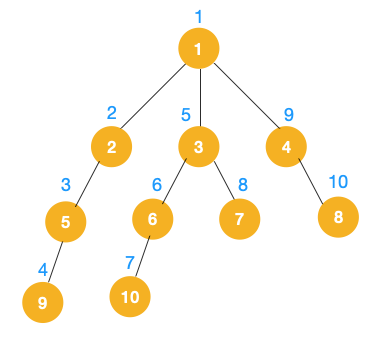
1、我们从根节点 1 开始遍历，它相邻的节点有 2，3，4，先遍历节点 2，再遍历 2 的子节点 5，然后再遍历 5 的子节点 9。

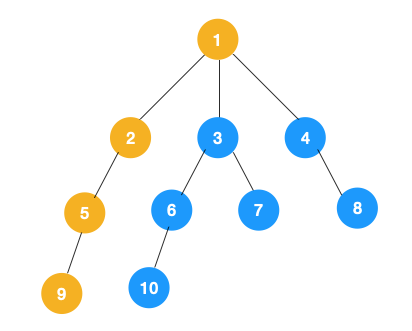
2、上图中一条路已经走到底了(9是叶子节点，再无可遍历的节点)，此时就从 9 回退到上一个节点 5，看下节点 5 是否还有除 9 以外的节点，没有继续回退到 2，2 也没有除 5 以外的节点，回退到 1，1 有除 2 以外的节点 3，所以从节点 3 开始进行深度优先遍历，如下：

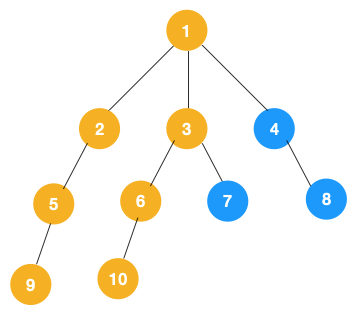
3、同理从 10 开始往上回溯到 6, 6 没有除 10 以外的子节点，再往上回溯，发现 3 有除 6 以外的子点 7，所以此时会遍历 7。

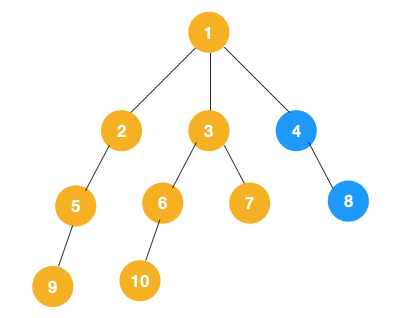
3、从 7 往上回溯到 3， 1，发现 1 还有节点 4 未遍历，所以此时沿着 4， 8 进行遍历,这样就遍历完成了。

完整的节点的遍历顺序如下(节点上的的蓝色数字代表)：

相信大家看到以上的遍历不难发现这就是树的前序遍历,实际上不管是前序遍历，还是中序遍历，亦或是后序遍历，都属于深度优先遍历。

那么深度优先遍历该怎么实现呢，有递归和非递归两种表现形式，接下来我们以二叉树为例来看下如何分别用递归和非递归来实现深度优先遍历。

1、递归实现

递归实现比较简单，由于是前序遍历，所以我们依次遍历当前节点，左节点，右节点即可，对于左右节点来说，依次遍历它们的左右节点即可，依此不断递归下去，直到叶节点(递归终止条件)，代码如下：

public class Solution {
    private static class Node {
        /**
         * 节点值
         */
        public int value;
        /**
         * 左节点
         */
        public Node left;
        /**
         * 右节点
         */
        public Node right;

        public Node(int value, Node left, Node right) {
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }

    public static void dfs(Node treeNode) {
        if (treeNode == null) {
            return;
        }
        // 遍历节点
        process(treeNode)
        // 遍历左节点
        dfs(treeNode.left);
        // 遍历右节点
        dfs(treeNode.right);
    }
}

递归的表达性很好，也很容易理解，不过如果层级过深，很容易导致栈溢出。所以我们重点看下非递归实现。

2、非递归实现

仔细观察深度优先遍历的特点，对二叉树来说，由于是先序遍历(先遍历当前节点，再遍历左节点，再遍历右节点)，所以我们有如下思路：

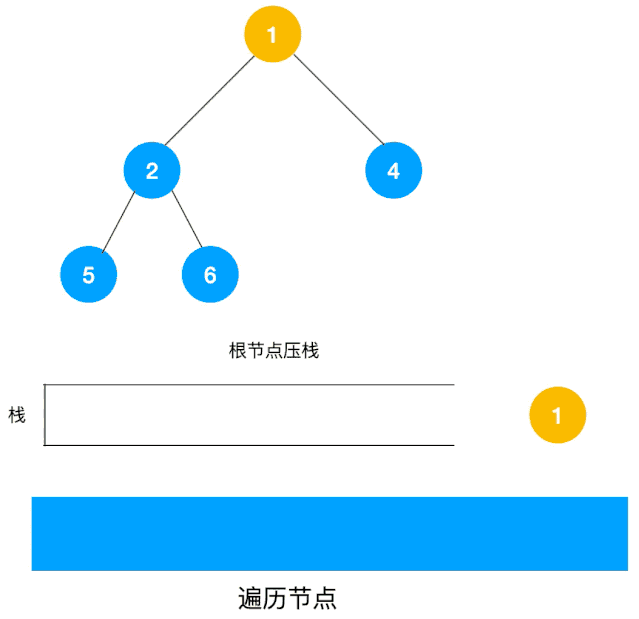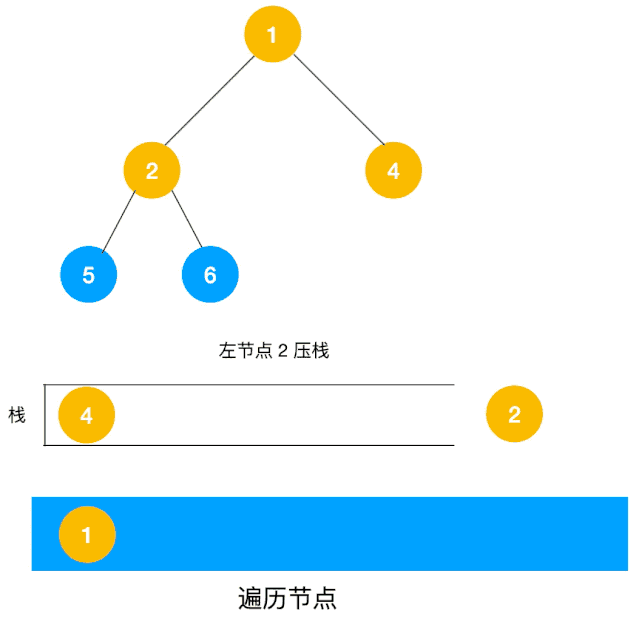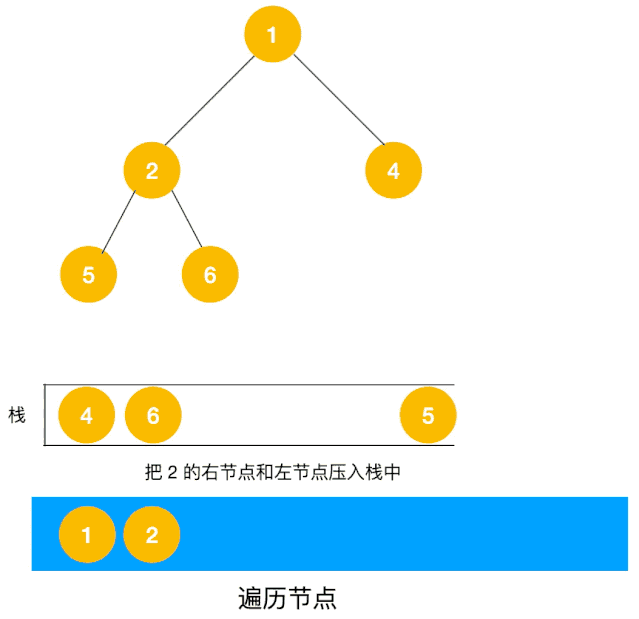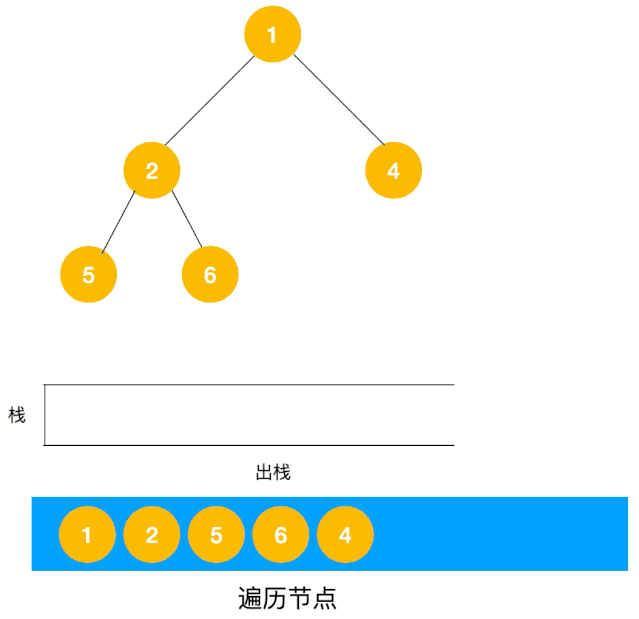
对于每个节点来说，先遍历当前节点，然后把右节点压栈，再压左节点(这样弹栈的时候会先拿到左节点遍历，符合深度优先遍历要求)。

弹栈，拿到栈顶的节点，如果节点不为空，重复步骤 1， 如果为空，结束遍历。

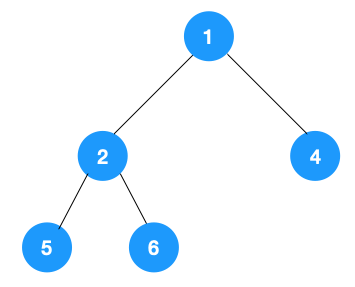
我们以以下二叉树为例来看下如何用栈来实现 DFS。

整体动图如下：

整体思路还是比较清晰的，使用栈来将要遍历的节点压栈，然后出栈后检查此节点是否还有未遍历的节点，有的话压栈，没有的话不断回溯(出栈)，有了思路，不难写出如下用栈实现的二叉树的深度优先遍历代码：

/**
 * 使用栈来实现 dfs
 * @param root
 */
public static void dfsWithStack(Node root) {
    if (root == null) {
        return;
    }

    Stack<Node> stack = new Stack<>();
    // 先把根节点压栈
    stack.push(root);
    while (!stack.isEmpty()) {
        Node treeNode = stack.pop();
        // 遍历节点
        process(treeNode)

        // 先压右节点
        if (treeNode.right != null) {
            stack.push(treeNode.right);
        }

        // 再压左节点
        if (treeNode.left != null) {
            stack.push(treeNode.left);
        }
    }
}

可以看到用栈实现深度优先遍历其实代码也不复杂，而且也不用担心递归那样层级过深导致的栈溢出问题。

广度优先遍历

广度优先遍历，指的是从图的一个未遍历的节点出发，先遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点。

上文所述树的广度优先遍历动图如下，每个节点的值即为它们的遍历顺序。所以广度优先遍历也叫层序遍历，先遍历第一层(节点 1)，再遍历第二层(节点 2，3，4)，第三层(5，6，7，8)，第四层(9，10)。

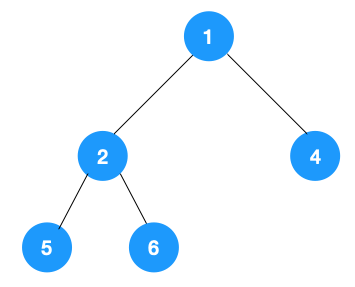
深度优先遍历用的是栈，而广度优先遍历要用队列来实现，我们以下图二叉树为例来看看如何用队列来实现广度优先遍历。

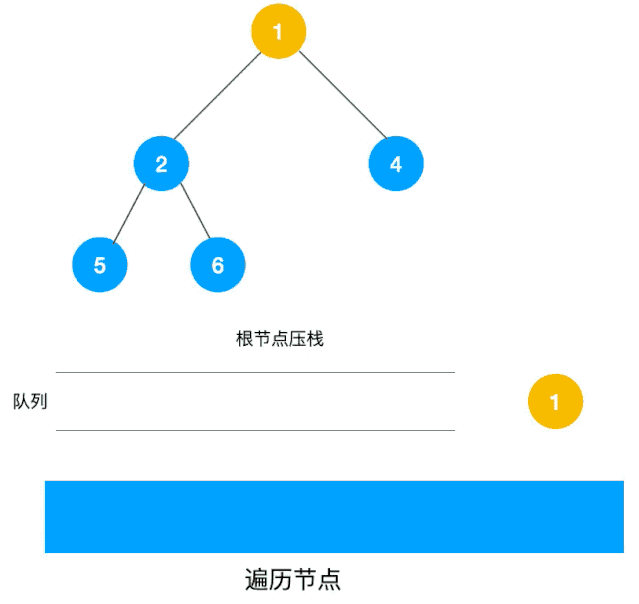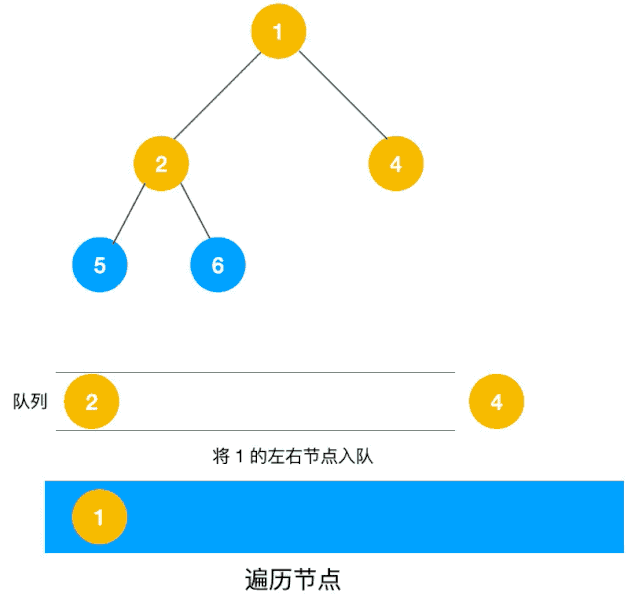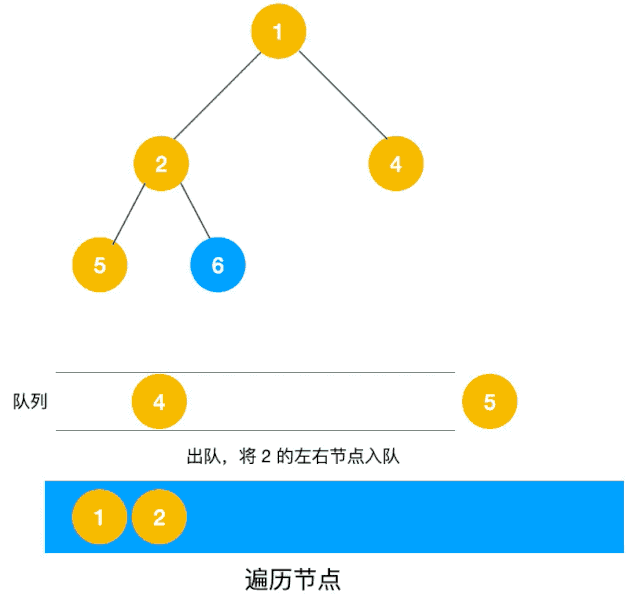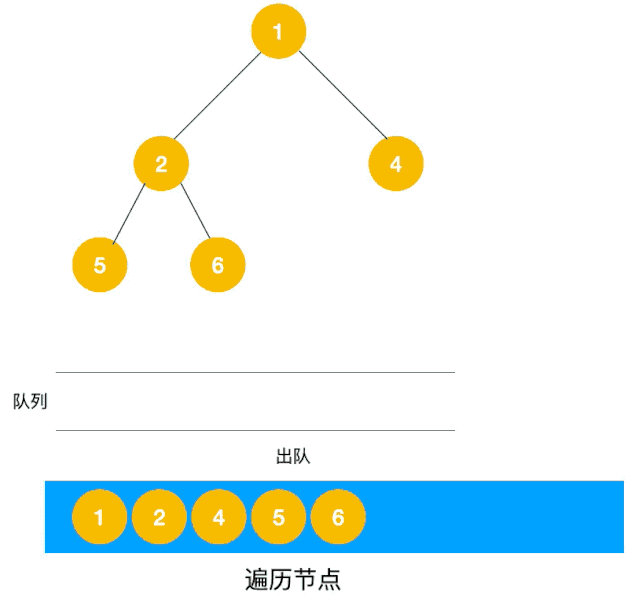
动图如下：

相信看了以上动图，不难写出如下代码：

/**
 * 使用队列实现 bfs
 * @param root
 */
private static void bfs(Node root) {
    if (root == null) {
        return;
    }
    Queue<Node> stack = new LinkedList<>();
    stack.add(root);

    while (!stack.isEmpty()) {
        Node node = stack.poll();
        System.out.println("value = " + node.value);
        Node left = node.left;
        if (left != null) {
            stack.add(left);
        }
        Node right = node.right;
        if (right != null) {
            stack.add(right);
        }
    }
}

习题演练

接下来我们来看看在 leetcode 中出现的一些使用 DFS，BFS 来解题的题目：

leetcode 104，111: 给定一个二叉树，找出其最大/最小深度。

例如：给定二叉树 [3,9,20,null,null,15,7],

3
  /
 9  20
   /
  15   7

则它的最小深度 2，最大深度 3。

解题思路：这题比较简单，只不过是深度优先遍历的一种变形，只要递归求出左右子树的最大/最小深度即可，深度怎么求，每递归调用一次函数，深度加一。不难写出如下代码：

/**
 * leetcode 104: 求树的最大深度
 * @param node
 * @return
 */
public static int getMaxDepth(Node node) {
    if (node == null) {
        return 0;
    }
    int leftDepth = getMaxDepth(node.left) + 1;
    int rightDepth = getMaxDepth(node.right) + 1;
    return Math.max(leftDepth, rightDepth);
}

/**
 * leetcode 111: 求树的最小深度
 * @param node
 * @return
 */
public static int getMinDepth(Node node) {
    if (node == null) {
        return 0;
    }
    int leftDepth = getMinDepth(node.left) + 1;
    int rightDepth = getMinDepth(node.right) + 1;
    return Math.min(leftDepth, rightDepth);
}

leetcode 102: 给你一个二叉树，请你返回其按层序遍历得到的节点值。(即逐层地，从左到右访问所有节点)。示例，给定二叉树：[3,9,20,null,null,15,7]。

3
  /
 9  20
   /
  15   7

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

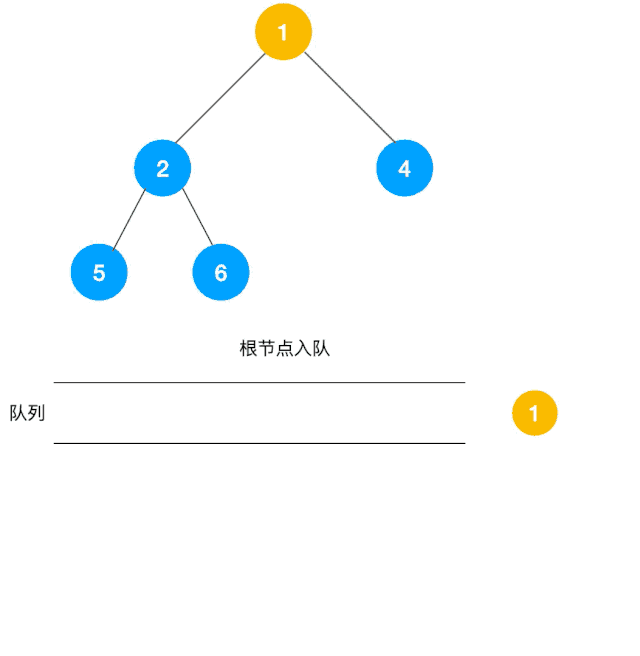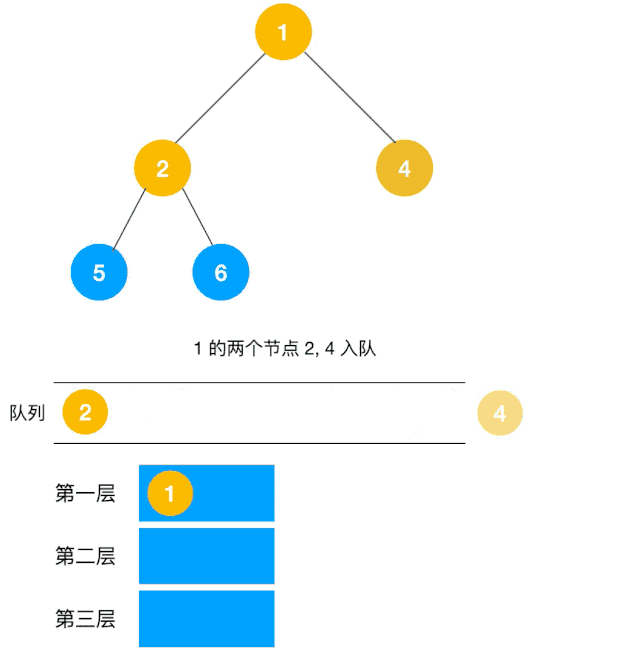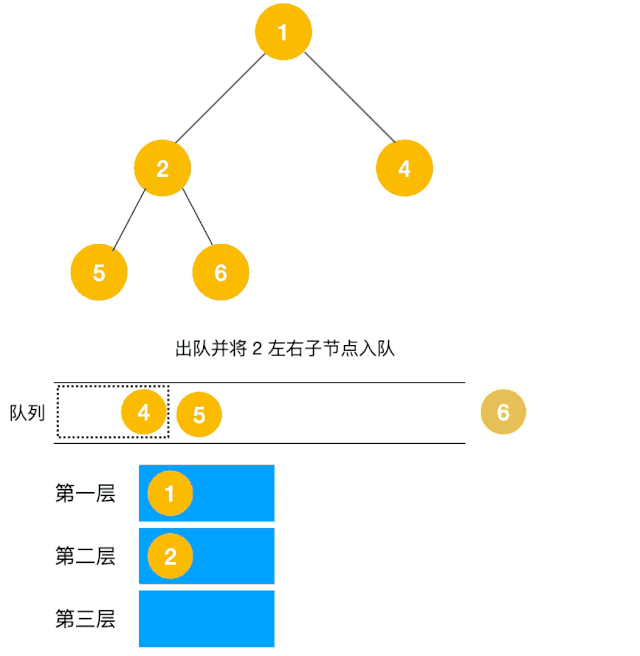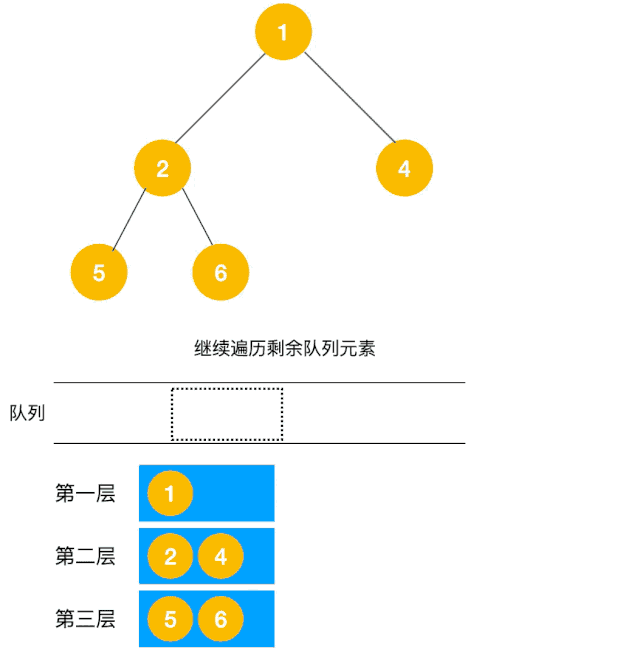
解题思路：显然这道题是广度优先遍历的变种，只需要在广度优先遍历的过程中，把每一层的节点都添加到同一个数组中即可，问题的关键在于遍历同一层节点前，必须事先算出同一层的节点个数有多少(即队列已有元素个数)，因为 BFS 用的是队列来实现的，遍历过程中会不断把左右子节点入队，这一点切记!动图如下：

根据以上动图思路不难得出代码如下：

Java 代码

/**
 * leetcdoe 102: 二叉树的层序遍历, 使用 bfs
 * @param root
 */
private static List<List<Integer>> bfsWithBinaryTreeLevelOrderTraversal(Node root) {
    if (root == null) {
        // 根节点为空，说明二叉树不存在，直接返回空数组
        return Arrays.asList();
    }

    // 最终的层序遍历结果
    List<List<Integer>> result = new ArrayList<>();

    Queue<Node> queue = new LinkedList<>();
    queue.offer(root);

    while (!queue.isEmpty()) {
        // 记录每一层
        List<Integer> level = new ArrayList<>();
        int levelNum = queue.size();
        // 遍历当前层的节点
        for (int i = 0; i < levelNum; i++) {
            Node node = queue.poll();
            // 队首节点的左右子节点入队,由于 levelNum 是在入队前算的，所以入队的左右节点并不会在当前层被遍历到
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
            level.add(node.value);
        }
        result.add(level);
    }

    return result;
}

Python 代码

class Solution:
    def levelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        res = []  #嵌套列表，保存最终结果
        if root is None:
            return res

        from collections import deque
        que = deque([root])  #队列，保存待处理的节点
        while len(que)!=0:
            lev = []  #列表，保存该层的节点的值
            thislevel = len(que)  #该层节点个数
            while thislevel!=0:
                head = que.popleft()  #弹出队首节点
                #队首节点的左右孩子入队
                if head.left is not None:
                    que.append(head.left)
                if head.right is not None:
                    que.append(head.right)
                lev.append(head.val)  #队首节点的值压入本层
                thislevel-=1
            res.append(lev)
        return res

这题用 BFS 是显而易见的，但其实也可以用 DFS， 如果在面试中能用 DFS 来处理，会是一个比较大的亮点。

用 DFS 怎么处理呢，我们知道， DFS 可以用递归来实现，其实只要在递归函数上加上一个「层」的变量即可，只要节点属于这一层，则把这个节点放入相当层的数组里，代码如下：

private static final List<List<Integer>> TRAVERSAL_LIST  = new ArrayList<>();
/**
 * leetcdoe 102: 二叉树的层序遍历, 使用 dfs
 * @param root
 * @return
 */
private static void dfs(Node root, int level) {
    if (root == null) {
        return;
    }

    if (TRAVERSAL_LIST.size() < level + 1) {
        TRAVERSAL_LIST.add(new ArrayList<>());
    }

    List<Integer> levelList = TRAVERSAL_LIST.get(level);
    levelList.add(root.value);

    // 遍历左结点
    dfs(root.left, level + 1);

    // 遍历右结点
    dfs(root.right, level + 1);
}

DFS，BFS 在搜索引擎中的应用我们几乎每天都在 Google, Baidu 这些搜索引擎，那大家知道这些搜索引擎是怎么工作的吗，简单来说有三步：

1、网页抓取

搜索引擎通过爬虫将网页爬取，获得页面 HTML 代码存入数据库中

2、预处理

索引程序对抓取来的页面数据进行文字提取，中文分词，(倒排)索引等处理，以备排名程序使用

3、排名

用户输入关键词后，排名程序调用索引数据库数据，计算相关性，然后按一定格式生成搜索结果页面。

我们重点看下第一步，网页抓取。

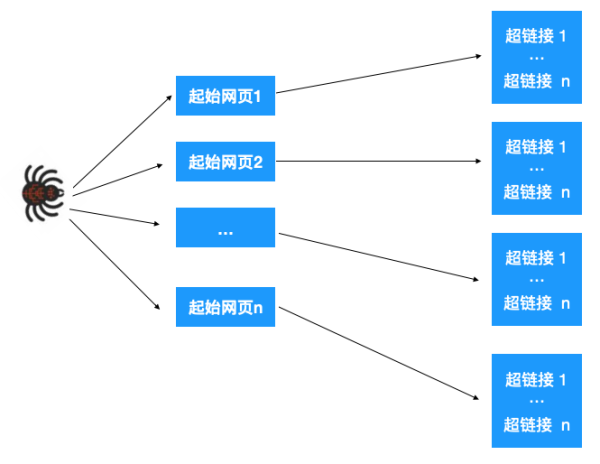
这一步的大致操作如下：给爬虫分配一组起始的网页，我们知道网页里其实也包含了很多超链接，爬虫爬取一个网页后，解析提取出这个网页里的所有超链接，再依次爬取出这些超链接，再提取网页超链接。。。，如此不断重复就能不断根据超链接提取网页。如下图示：

如上所示，最终构成了一张图，于是问题就转化为了如何遍历这张图，显然可以用深度优先或广度优先的方式来遍历。

如果是广度优先遍历，先依次爬取第一层的起始网页，再依次爬取每个网页里的超链接，如果是深度优先遍历，先爬取起始网页 1，再爬取此网页里的链接...，爬取完之后，再爬取起始网页 2...

实际上爬虫是深度优先与广度优先两种策略一起用的，比如在起始网页里，有些网页比较重要(权重较高)，那就先对这个网页做深度优先遍历，遍历完之后再对其他(权重一样的)起始网页做广度优先遍历。

总结

DFS 和 BFS 是非常重要的两种算法，大家一定要掌握，本文为了方便讲解，只对树做了 DFS，BFS，大家可以试试如果用图的话该怎么写代码，原理其实也是一样，只不过图和树两者的表示形式不同而已，DFS 一般是解决连通性问题，而 BFS 一般是解决最短路径问题，之后有机会我们会一起来学习下并查集，Dijkstra, Prism 算法等，敬请期待!