pat甲级1002

1002. A+B for Polynomials (25)

时间限制

400 ms

内存限制

65536 kB

代码长度限制

16000 B

判题程序

Standard

作者

CHEN, Yue

This time, you are supposed to find A+B where A and B are two polynomials.

Input

Each input file contains one test case. Each case occupies 2 lines, and each line contains the information of a polynomial: K N1 a_N1 N2 a_N2 ... NK a_NK, where K is the number of nonzero terms in the polynomial, Ni and a_Ni (i=1, 2, ..., K) are the exponents and coefficients, respectively. It is given that 1 <= K <= 10，0 <= NK < ... < N2 < N1 <=1000.

Output

For each test case you should output the sum of A and B in one line, with the same format as the input. Notice that there must be NO extra space at the end of each line. Please be accurate to 1 decimal place.

Sample Input

2 1 2.4 0 3.2
2 2 1.5 1 0.5

Sample Output

3 2 1.5 1 2.9 0 3.2

#include<cstdio>
struct node
{
    int e;//指数
    double cof;//系数
}a[1500],b[1500];
double ans[2002]={0};
int main()
{
    int m,n,sum=0;
    scanf("%d",&m);
    for(int i=0;i<m;i++)
    {
        scanf("%d %lf",&a[i].e,&a[i].cof);
        ans[a[i].e]+=a[i].cof;
    }
    scanf("%d",&n);
    sum=m+n;
    for(int i=0;i<n;i++)
    {
        scanf("%d %lf",&b[i].e,&b[i].cof);
        ans[b[i].e]+=b[i].cof;
    }
    for(int i=0;i<m;i++)
    {
        for(int j=0;j<n;j++)
        {
            if(a[i].e==b[j].e)
                sum--;
        }
    }

    printf("%d",sum);
    for(int i=2000;i>=0;i--)
    {
        if(ans[i]!=0)
            printf(" %d %.1lf",i,ans[i]);
    }


    return 0;
}

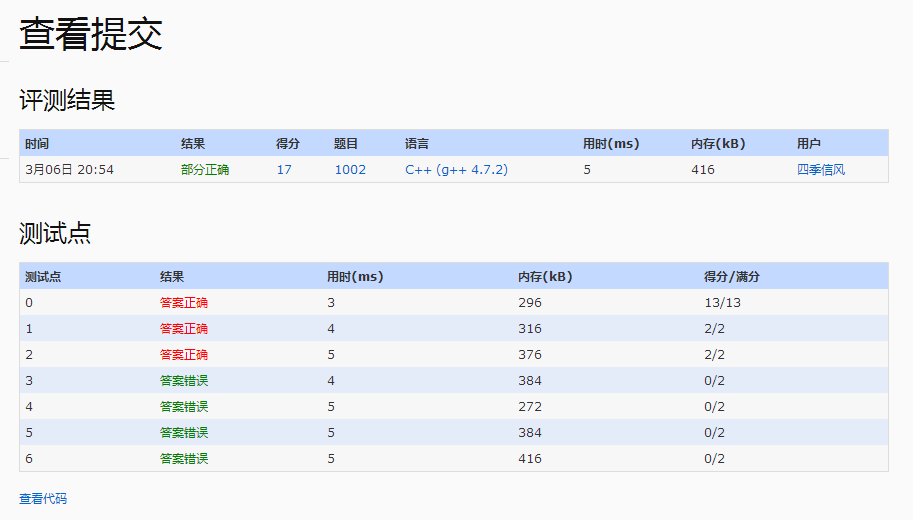
有四个测试点过不去，应该是最后计含有非零项多项式时候少考虑了一种情况——两个指数相同的项的系数和为0

#include<cstdio>
struct node
{
	int e;//指数
	double cof;//系数
}a[1500],b[1500];
double ans[2002]={0};
int main()
{
	int m,n,sum=0;
	scanf("%d",&m);
	for(int i=0;i<m;i++)
	{
		scanf("%d %lf",&a[i].e,&a[i].cof);
		ans[a[i].e]+=a[i].cof;
	}
	scanf("%d",&n);
	sum=m+n;
	for(int i=0;i<n;i++)
	{
		scanf("%d %lf",&b[i].e,&b[i].cof);
		ans[b[i].e]+=b[i].cof;
	}
	for(int i=0;i<m;i++)
	{
		for(int j=0;j<n;j++)
		{
			if(a[i].e==b[j].e)
				sum--;
			if(a[i].e==b[j].e&&a[i].cof+b[j].cof==0)
				sum--;
		}
	}

	printf("%d",sum);
	for(int i=2000;i>=0;i--)
	{
		if(ans[i]!=0)
			printf(" %d %.1lf",i,ans[i]);
	}


	return 0;
}

　改动一段代码果然解决了问题