51nod1043 幸运号码

---

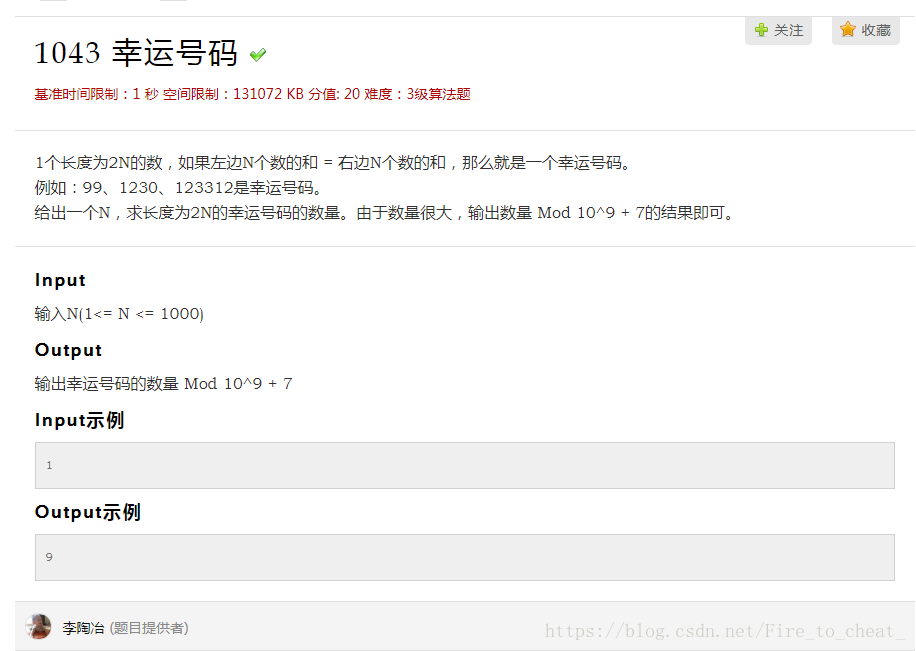
数位DP：
dp[i][j]表示i*2位和为j的数的个数
状态转移方程：
dp[i][j]=dp[i][j]+dp[i-1][j-k]
最后
用 去掉0*没有去掉0 取模
((dp[n][i]-dp[n-1][i])*dp[n][i])%MOD

#include <bits/stdc++.h>

using namespace std;
#define LL long long
const int MOD =1e9+7;
const int MAXN= 1005;


LL dp[MAXN][MAXN*9];//长度为i和为j的个数





/*
dp[i][j]=(dp[i][j]+dp[i-1][j-k]
去掉前导0：
dp[n][i]-dp[n-1][i]


*/

int main()
{
    LL ans=0;
    int n;
    cin>>n;
    dp[0][0]=1;//前导0
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=i*9;j++)
        {
            for(int k=0;k<=9;k++)
            {
                if(j>=k)
                {
                    dp[i][j]=(dp[i][j]+dp[i-1][j-k])%MOD;
                }
                else
                {
                    break;
                }
            }
        }
    }
    for(int i=0;i<=9*n;i++)
    {
        ans=(ans+(dp[n][i]-dp[n-1][i])*dp[n][i])%MOD;
    }
    cout<<ans<<endl;
    return 0;
}