思路:对于一个奇数,可以先自减1变成偶数后,得到可以减其自身的一个数,算出步骤数
然后用线段树进行区间查询
#include<iostream>
#include<cstdio>
using namespace std;
#define ll long long
const int maxn=100005;
ll sum[maxn<<2],a[maxn];
int getN(ll temp)
{
int ans=0;
while(temp!=0){
if(temp%2==1){
temp--;
}else
temp/=2;
ans++;
}
return ans-1;
}
void pushup(int rt)//回溯(节点为两个子树之和)
{
sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
/*build函数是从底层建树,一直回溯到根节点,自己推导可以从根节点依次二分展开整个树*/
void build(int l,int r,int rt)
{//[l,r]表示当前节点区间,rt表示当前节点的实际存储位置
if(l==r){//若到达叶节点
sum[rt]=a[l];
return;
}
int m=(l+r)>>1;
//左右递归
build(l,m,rt<<1);
build(m+1,r,rt<<1|1);
pushup(rt);
}
void update(int L,int C,int l,int r,int rt)
{//[l,r]表示当前区间,rt是当前节点编号
if(l==r){//到达叶节点,修改叶节点的值
sum[rt]=C;
return;
}
int m=(l+r)>>1;
//根据条件判断往左子树调用还是右
if(L<=m)
update(L,C,l,m,rt<<1);
else
update(L,C,m+1,r,rt<<1|1);
pushup(rt);//子节点的信息更新了,所以本节点也要更新信息
}
int query(int L,int R,int l,int r,int rt)
{//[L,R]表示要获取区间,[l,r]表示当前区间,rt:当前节点编号
if(L<=l&&r<=R){ //在区间内直接返回
return sum[rt];
}
int m=(l+r)>>1;
//左子区间:[l,m] 右子区间:[m+1,r] 求和区间:[L,R]
//累加答案
int ans=0;
if(L<=m){
int temp=query(L,R,l,m,rt<<1);//左子区间与[L,R]有重叠,递归
ans=temp+ans;
}
if(R>m){
int temp=query(L,R,m+1,r,rt<<1|1);//右子区间与[L,R]有重叠,递归
ans=temp+ans;
}
return ans;
}
int main()
{
// freopen("in.txt","r",stdin);
int i,x,y;
int m,n,T,q;
ll temp;
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&q);
for(i=1;i<=n;i++){
scanf("%lld",&temp);
a[i]=getN(temp);
// cout<<a[i]<<endl;
}
build(1,n,1);//开始建树
while(q--)
{
scanf("%d%d",&x,&y);
printf("%d
",query(x,y,1,n,1));
}
}
}
第二类 求矩形并的面积
|
Atlantis
Description
There are several ancient Greek texts that contain descriptions of the fabled island Atlantis. Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the
total area for which maps exist. You (unwisely) volunteered to write a program that calculates this quantity.
Input
The input consists of several test cases. Each test case starts with a line containing a single integer n (1 <= n <= 100) of available maps. The n following lines describe one map each. Each of these lines contains four numbers x1;y1;x2;y2 (0 <= x1 < x2 <=
100000;0 <= y1 < y2 <= 100000), not necessarily integers. The values (x1; y1) and (x2;y2) are the coordinates of the top-left resp. bottom-right corner of the mapped area.
The input file is terminated by a line containing a single 0. Don't process it. Output
For each test case, your program should output one section. The first line of each section must be "Test case #k", where k is the number of the test case (starting with 1). The second one must be "Total explored area: a", where a is the total explored area
(i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point.
Output a blank line after each test case. Sample Input 2 10 10 20 20 15 15 25 25.5 0 Sample Output Test case #1 Total explored area: 180.00 Source |
[Submit] [Go Back] [Status] [Discuss]
/*
* 本题中的坐标是浮点类型的, 故不能将坐标直接离散.我们必须为它们建立一个对应关系,
* 用一个整数去对应一个浮点数这样的对应关系在本题的数组y[]中。
*/
struct node
{
int st, ed, c; // c: 区间被覆盖的层数, m: 区间的测度
double m;
} ST[802];
struct line
{
double x, y1, y2; // 纵方向直线, x:直线横坐标, y1 y2:直线上的下面与上面的两个纵坐标
bool s; // s = 1 : 直线为矩形的左边, s = 0:直线为矩形的右边
} Line[205];
double y[205], ty[205]; // y[]整数与浮点数的对应数组; ty[]:用来求y[]的辅助数组
void build(int root, int st, int ed)
{
ST[root].st = st;
ST[root].ed = ed;
ST[root].c = 0;
ST[root].m = 0;
if (ed - st > 1)
{
int mid = (st + ed) / 2;
build(root * 2, st, mid);
build(root * 2 + 1, mid, ed);
}
return ;
}
void updata(int root)
{
if (ST[root].c > 0)
{ // 将线段树上区间的端点分别映射到y[]数组所对应的浮点数上,由此计算出测度
ST[root].m = y[ST[root].ed - 1] - y[ST[root].st - 1];
}
else if (ST[root].ed - ST[root].st == 1)
{
ST[root].m = 0;
}
else
{
ST[root].m = ST[root * 2].m + ST[root * 2 + 1].m;
}
return ;
}
void insert(int root, int st, int ed)
{
if (st <= ST[root].st && ST[root].ed <= ed)
{
ST[root].c++;
updata(root);
return ;
}
if (ST[root].ed - ST[root].st == 1)
{
return ; // 不出错的话 这句话就是冗余的
}
int mid = (ST[root].ed + ST[root].st) / 2;
if (st < mid)
{
insert(root * 2, st, ed);
}
if (ed > mid)
{
insert(root * 2 + 1, st, ed);
}
updata(root);
return ;
}
void Delete(int root, int st, int ed)
{
if (st <= ST[root].st && ST[root].ed <= ed)
{
ST[root].c--;
updata(root);
return ;
}
if (ST[root].ed - ST[root].st == 1)
{
return ; // 不出错的话 这句话就是冗余的
}
int mid = (ST[root].st + ST[root].ed) / 2;
if (st < mid)
{
Delete(root * 2, st, ed);
}
if (ed > mid)
{
Delete(root * 2 + 1, st, ed);
}
updata(root);
return ;
}
int Correspond(int n, double t)
{
// 二分查找出浮点数t在数组y[]中的位置(此即所谓的映射关系)
int low, high, mid;
low = 0;
high = n - 1;
while (low < high)
{
mid = (low + high) / 2;
if (t > y[mid])
{
low = mid + 1;
}
else
{
high = mid;
}
}
return high + 1;
}
bool cmp(line l1, line l2)
{
return l1.x < l2.x;
}
int main()
{
int n, i, num, l, r, c = 0;
double area, x1, x2, y1, y2;
while (cin >> n, n)
{
for (i = 0; i < n; i++)
{
cin >> x1 >> y1 >> x2 >> y2;
Line[2 * i].x = x1;
Line[2 * i].y1 = y1;
Line[2 * i].y2 = y2;
Line[2 * i].s = 1;
Line[2 * i + 1].x = x2;
Line[2 * i + 1].y1 = y1;
Line[2 * i + 1].y2 = y2;
Line[2 * i + 1].s = 0;
ty[2 * i] = y1;
ty[2 * i + 1] = y2;
}
n <<= 1;
sort(Line, Line + n, cmp);
sort(ty, ty + n);
y[0] = ty[0];
// 处理数组ty[]使之不含重覆元素,得到新的数组存放到数组y[]中
for (i = num = 1; i < n; i++)
{
if (ty[i] != ty[i - 1])
{
y[num++] = ty[i];
}
}
build(1, 1, num); // 树的叶子节点与数组y[]中的元素个数相同,以便建立一一对应的关系
area = 0;
for (i = 0; i < n - 1; i++)
{ // 由对应关系计算出线段两端在树中的位置
l = Correspond(num, Line[i].y1);
r = Correspond(num, Line[i].y2);
if (Line[i].s) // 插入矩形的左边
{
insert(1, l, r);
}
else // 删除矩形的右边
{
Delete(1, l, r);
}
area += ST[1].m * (Line[i + 1].x - Line[i].x);
}
cout << "Test case #" << ++c << endl << "Total explored area: ";
cout << fixed << setprecision(2) << area << endl << endl; // 需要引入iomanip头文件
}
return 0;
}第三类 求矩形并的周长(线段树+离散化+扫描线)
|
Picture
Description
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of
all rectangles is called the perimeter.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1. 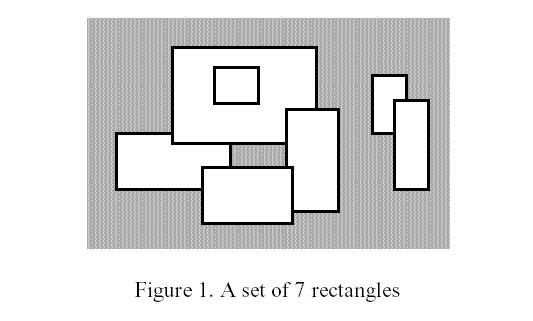 The corresponding boundary is the whole set of line segments drawn in Figure 2. 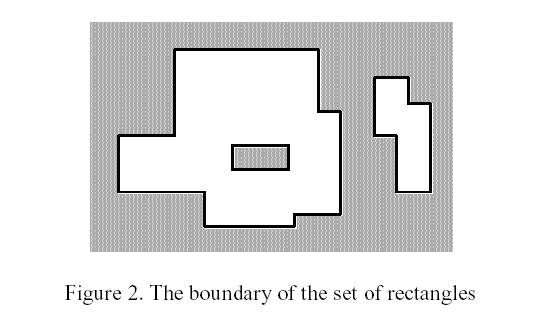 The vertices of all rectangles have integer coordinates. Input
Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The
values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.
0 <= number of rectangles < 5000 All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area. Output
Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.
Sample Input 7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16 Sample Output 228 Source |
[Submit] [Go Back] [Status] [Discuss]
struct node
{
int st, ed, m, lbd, rbd;
int sequence_line, count;
} ST[40005];
void build(int st, int ed, int v) // 建树,区间为[st, ed]
{
ST[v].st = st;
ST[v].ed = ed;
ST[v].m = ST[v].lbd = ST[v].rbd = 0;
ST[v].sequence_line = ST[v].count = 0;
if (ed - st > 1)
{
int mid = (st + ed) / 2;
build(st, mid, 2 * v + 1);
build(mid, ed, 2 * v + 2);
}
return ;
}
void UpData(int v) // 更新结点区间的测度
{
if (ST[v].count > 0)
{
ST[v].m = ST[v].ed - ST[v].st;
ST[v].lbd = ST[v].rbd = 1;
ST[v].sequence_line = 1;
return ;
}
if (ST[v].ed - ST[v].st == 1)
{
ST[v].m = 0;
ST[v].lbd = ST[v].rbd = 0;
ST[v].sequence_line = 0;
}
else
{
int left = 2 * v + 1, right = 2 * v + 2;
ST[v].m = ST[left].m + ST[right].m;
ST[v].sequence_line = ST[left].sequence_line + ST[right].sequence_line - (ST[left].rbd & ST[right].lbd);
ST[v].lbd = ST[left].lbd;
ST[v].rbd = ST[right].rbd;
}
return ;
}
void insert(int st, int ed, int v)
{
if (st <= ST[v].st && ed >= ST[v].ed)
{
ST[v].count++;
UpData(v);
return ;
}
int mid = (ST[v].st + ST[v].ed) / 2;
if (st < mid)
{
insert(st, ed, 2 * v + 1);
}
if (ed > mid)
{
insert(st, ed, 2 * v + 2);
}
UpData(v);
return ;
}
void Delete(int st, int ed, int v)
{
if (st <= ST[v].st && ed >= ST[v].ed)
{
ST[v].count--;
UpData(v);
return ;
}
int mid = (ST[v].st + ST[v].ed) / 2;
if (st < mid)
{
Delete(st, ed, 2 * v + 1);
}
if (ed > mid)
{
Delete(st, ed, 2 * v + 2);
}
UpData(v);
return ;
}
struct line
{
int x, y1, y2; // y1 < y2
bool d; // d=true表示该线段为矩形左边,d=false表示该线段为矩形的右边
} a[10003];
bool cmp(line t1, line t2) // 为线段排序的函数,方便从左向右的扫描
{
return t1.x < t2.x;
}
void cal_C(int n);
int main()
{
int n, x1, x2, y1, y2, i, j, suby, upy;
while (scanf("%d",&n) != EOF)
{
j = 0;
suby = 10000;
upy = -10000;
for (i = 0; i < n; i++)
{
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
a[j].x = x1;
a[j].y1 = y1;
a[j].y2 = y2;
a[j].d = 1;
j++;
a[j].x = x2;
a[j].y1 = y1;
a[j].y2 = y2;
a[j].d = 0;
j++;
if (suby > y1)
{
suby = y1;
}
if (upy < y2)
{
upy = y2;
}
}
sort(a, a + j, cmp);
build(suby, upy, 0);
cal_C(j);
}
return 0;
}
void cal_C(int n)
{
int i, t2, sum = 0;
t2 = 0;
a[n] = a[n - 1];
for (i = 0; i < n; i++)
{
if (a[i].d == 1)
{
insert(a[i].y1, a[i].y2, 0);
}
else
{
Delete(a[i].y1, a[i].y2, 0);
}
sum += ST[0].sequence_line * (a[i + 1].x - a[i].x) * 2;
sum += abs(ST[0].m - t2);
t2 = ST[0].m;
}
printf("%d
", sum);
}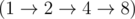 .
Also, you can build number 10 starting from 1 with five operations
.
Also, you can build number 10 starting from 1 with five operations 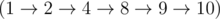 .
.