
样例输入
2 2 1 1 3 1 2
样例输出
500000004 555555560
思路:
n重伯努利实验概率分布题。 设q=1-p,p为事件概率。 Y为出现偶数次的概率。
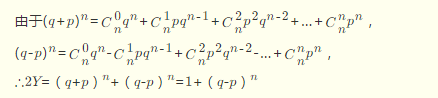
所以 Y=1/2*((1-2*p)^n+1)
先求快速幂,再求逆元
#include<bits/stdc++.h>
#define LL long long
#define mod 1000000007
using namespace std;
LL quick_pow(LL x, LL n) {
LL res = 1;
x=(x%mod+mod)%mod;
while(n) {
if(n&1)
res=res*x% mod;
n >>=1;
x =x*x% mod;
}
return res;
}
int main()
{
LL p, q;
LL n;
int t;
scanf("%d", &t);
while(t --) {
scanf("%lld%lld%lld",&p, &q, &n);
LL a=quick_pow(p,mod-2);
a=(a*2*q)%mod;
a=(1-a+mod)%mod;
a=quick_pow(a,n)%mod;
a=(a+1)%mod;
LL b=quick_pow(2,mod-2)%mod;
a=(a*b)%mod;
printf("%lld
", (a%mod+mod)%mod);
}
}