单源最短路径问题,即在图中求出给定顶点到其它任一顶点的最短路径。在弄清楚如何求算单源最短路径问题之前,必须弄清楚最短路径的最优子结构性质。
一.最短路径的最优子结构性质
该性质描述为:如果P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,k和s是这条路径上的一个中间顶点,那么P(k,s)必定是从k到s的最短路径。下面证明该性质的正确性。
假设P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是从k到s的最短距离,那么必定存在另一条从k到s的最短路径P'(k,s),那么P'(i,j)=P(i,k)+P'(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。
二.Dijkstra算法
由上述性质可知,如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点。那么(Vi...Vk)也必定是从i到k的最短路径。为了求出最短路径,Dijkstra就提出了以最短路径长度递增,逐次生成最短路径的算法。譬如对于源顶点V0,首先选择其直接相邻的顶点中长度最短的顶点Vi,那么当前已知可得从V0到达Vj顶点的最短距离dist[j]=min{dist[j],dist[i]+matrix[i][j]}。
根据这种思路,假设存在G=<V,E>,源顶点为V0,U={V0},dist[i]记录V0到i的最短距离,path[i]记录从V0到i路径上的i前面的一个顶点。
1.从V-U中选择使dist[i]值最小的顶点i,将i加入到U中;
2.更新与i直接相邻顶点的dist值。(dist[j]=min{dist[j],dist[i]+matrix[i][j]})
3.知道U=V,停止。
用下面这幅图来做示例。

设1为起点,则与1相邻的点为2、3、4。距离分别为100、30、10。对1进行标记,后续不在参加比较。在以上个点进行标注距离,并比较参加比较的点的距离大小。
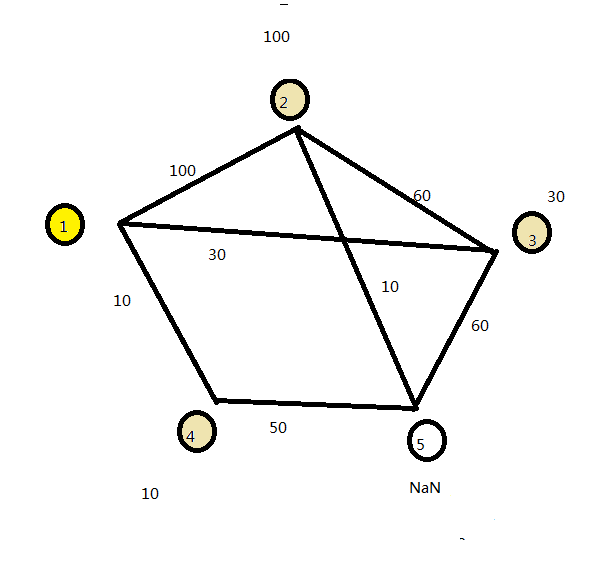
得出4的距离最小。标记4,后续不参加比较。
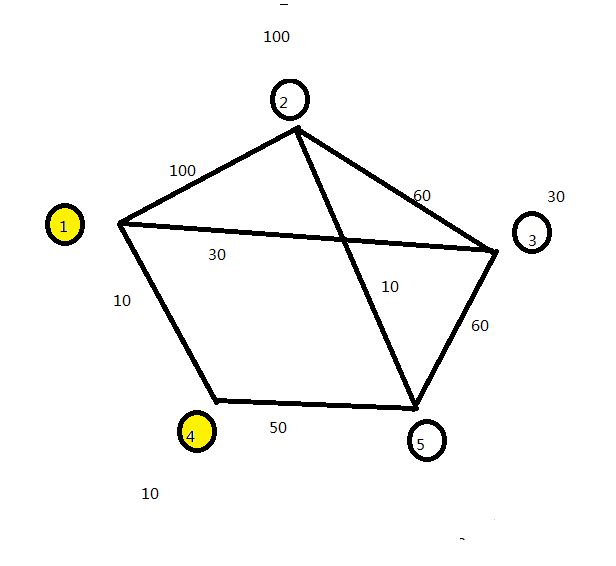
与4相邻的点5,重新计算距离。因为5距1的距离无限大。相邻点4为距1最短的路径,在加上4与5之间的距离得5的距离为60。
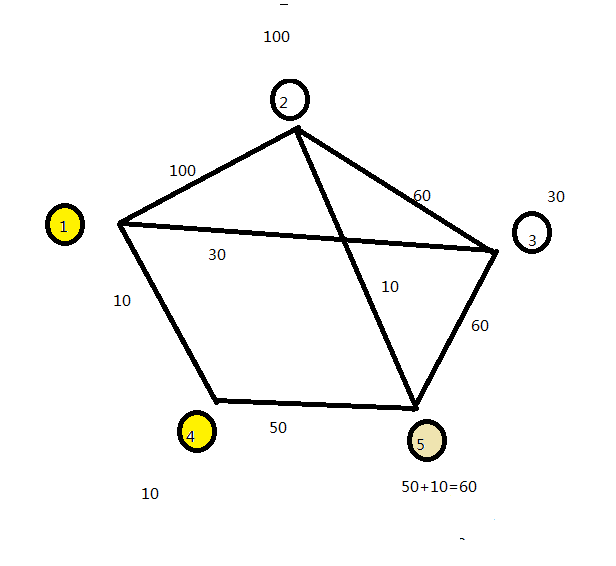
在未标记点中找最小的,得到3最小,对3进行标记,后续不参加比较。3的相邻点为2和5。2经由3的距离为90比原距离短,对2进行更新。5经由3的距离为90,比原来长,不进行更新。
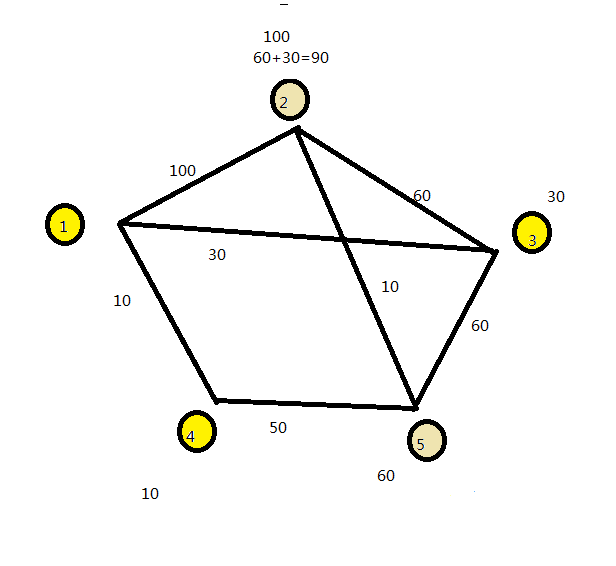
更新后未标记的点进行比较,5更小,标记5。
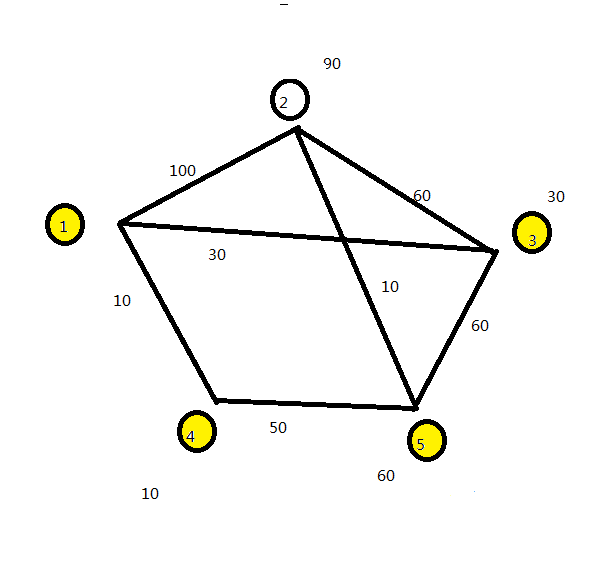
2经由5的距离为70,比原来小,对2进行更新。
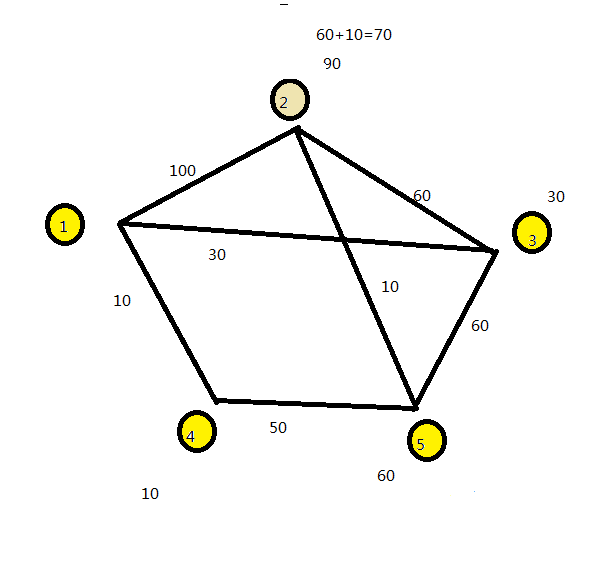
至此,所有点到1的最短距离就得到了。
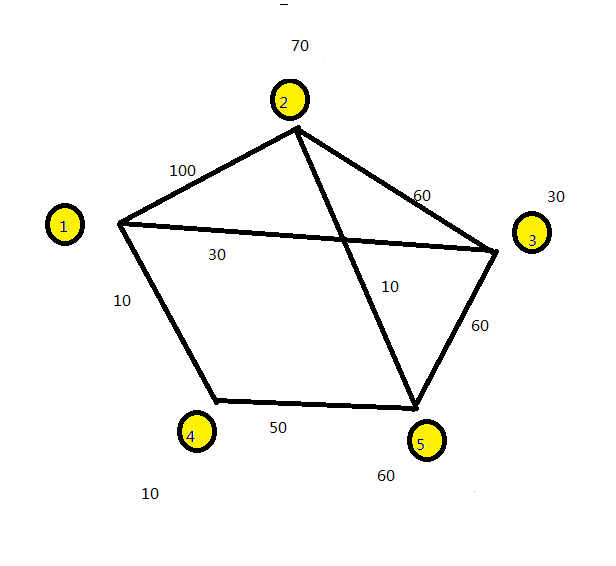
上代码,写的比较急,容错不好,主要看下算法实现部分
#include <stdio.h> #include <iostream> using namespace std; int main(int argc, char** argv) { int nodeNum = 0;//顶点数 int argMatix[50][50] = {0};//个顶点之间的距离 int dist[50] = {0};//顶点到起始点的距离 int i,j; cout<<"请输入顶点数"<<endl; cin>>nodeNum;//输入顶点数 for(i=0;i<nodeNum;i++) { dist[i] = 9999;//初始化个顶点到起始点的距离为无穷大 for(j=0;j<nodeNum;j++) { argMatix[i][j]=9999;//初始化各顶点之间的距离为无穷大 } } cout<<"请输入提示两点间的距离,如提示为1,2,则输入1和2之间的距离。两点间没有直接连线请输入9999。(顶点编号从0开始)"<<endl; for(i=0;i<nodeNum;i++) { for(j=0;j<nodeNum;j++) { cout<<i<<","<<j<<":"; if(i==j)//顶点到自己的距离为0 { argMatix[i][j] = argMatix[j][i] = 0; cout<<argMatix[j][i]<<endl; } else if(argMatix[j][i]!=9999)//a顶点到b顶点的距离已经输入,那么b到a的距离就等于a到b的距离了 { argMatix[i][j] = argMatix[j][i]; cout<<argMatix[j][i]<<endl; } else//输入顶点间的距离 { cin>>argMatix[i][j]; } } } cout<<"---------------"<<endl; cout<<"请输入起始点"<<endl; int beginNode = 0;//起始点 cin>>beginNode;//输入起始点 bool flg[50]={false};//后续是否参与比较 flg[beginNode] = true;//起始点加入不参与比较里 dist[beginNode] = 0;//起始点距起始点的距离为0 int lastNode = beginNode;//最新标记的点 //------------------------------------------- //数据输入结束 //算法开始 for(j=0;j<nodeNum;j++)//重新遍历所有点 { for(i=0;i<nodeNum;i++)//遍历所有点 { if(flg[i])//已经标记过不参加比较 continue; if(dist[i]>argMatix[i][lastNode]+dist[lastNode])//如果i点到起始点的距离 比上一个标记的点和它之间的距离加上一个标记的点到起始点的距离 还大 { dist[i] = argMatix[i][lastNode]+dist[lastNode];//更新i点到起始点的距离 } } int minindex = -1;//比较点中最小的那个 for(i=0;i<nodeNum;i++)//遍历所有点 { if(flg[i])//已标记过不参加比较 continue; if(minindex==-1)//第一次进入 { minindex = i;//直接标为最小点 continue; } if(dist[i]<dist[minindex])//找到新的距离最小的那个点 { minindex = i; } } if(minindex!=-1)//找到了到起始点距离最小的那个点 { flg[minindex] = true;//后续不参加比较 lastNode = minindex;//该点为最后标记的点 } } //所有点都标记过了 for(i=0;i<nodeNum;i++) { cout<<i<<"到起始点的最短距离为:"<<dist[i]<<endl;//打印到起始点的距离 } }