该文档转载自图像缩放——双线性插值算法,我搜罗一堆中文文章里面讲得比较清楚的一篇了。
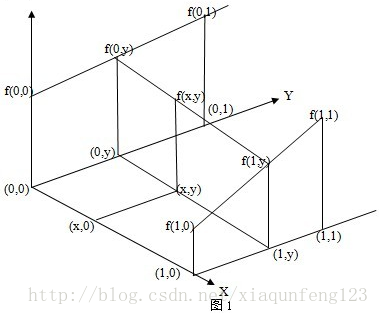
在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。如果选择一个坐标系统使得 f 的四个已知点坐标分别为 (0, 0),(0, 1),(1, 0) 和 (1, 1),那么插值公式就可以化简为
用矩阵运算来表示的话就是

图像的空间变换,也称几何变换或几何运算,包括图像的平移、旋转、镜像变换、转置、缩放等。空间变换可如下表示:设(u,v)为源图像上的点,(x,y)为目标图像上的点,则空间变换就是将源图像上(u,v)处的颜色值与目标图像上(x,y)处的颜色对应起来。
计算机所处理的图像都是指点阵图,也就是用一个像素矩阵来描述一副图像。举个简单的图像:3×3的256级灰度图,也就是高为3个象素,宽也是3个象素的图像,每个象素的取值可以是 0-255,代表该像素的亮度,255代表最亮,也就是白色,0代表最暗,即黑色 。
假如图像的象素矩阵如下所示:(这个矩阵中,图象处理中最常用的坐标系是:x从左到右,从0开始,y从上到下,也是从0开始)

如果想把这副图放大为 4X4大小的图像,那么第一步肯定想到的是先把4X4的矩阵先画出来再说,好了矩阵画出来了,如下所示,当然,矩阵的每个像素都是未知数,等待着我们去填充

然后要往这个空的矩阵里面填值了,要填的值从哪里来来呢?是从源图中来,好,先填写目标图最左上角的象素,坐标为(0,0),那么该坐标对应源图中的坐标可以由如下公式得出:
套用公式,就可以找到对应的原图的坐标了((0*(3/4),0*(3/4))=>(0*0.75,0*0.75)=>(0,0)),找到了源图的对应坐标,就可以把源图中坐标为(0,0)处的234象素值填进去目标图的(0,0)这个位置了。所有的数值填充之后的结果如下所示

这种放大图像的方法叫做最临近插值算法,这是一种最基本、最简单的图像缩放算法,效果也是最不好的,放大后的图像有很严重的马赛克,缩小后的图像有很严重的失真;效果不好的根源就是其简单的最临近插值方法引入了严重的图像失真。比如,当由目标图的坐标反推得到的源图的的坐标是一个浮点数的时候,采用了四舍五入的方法,直接采用了和这个浮点数最接近的象素的值,这种方法是很不科学的,当推得坐标值为 0.75的时候,不应该就简单的取为1,既然是0.75,比1要小0.25 ,比0要大0.75 ,那么目标象素值其实应该根据这个源图中虚拟的点四周的四个真实的点来按照一定的规律计算出来的,这样才能达到更好的缩放效果。
双线型内插值算法就是一种比较好的图像缩放算法,它充分的利用了源图中虚拟点四周的四个真实存在的像素值来共同决定目标图中的一个像素值,因此缩放效果比简单的最邻近插值要好很多,计算量比零阶插值大,但缩放后图像质量高,不会出现像素值不连续的情况。
双线性内插值算法描述如下:
对于一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v) (其中i、j均为浮点坐标的整数部分,u、v为浮点坐标的小数部分,是取值[0,1)区间的浮点数),则这个像素得值 f(i+u,j+v) 可由原图像中坐标为 (i,j),(i+1,j),(i,j+1),(i+1,j+1)所对应的周围四个像素的值决定,即:
其中f(i,j)表示源图像(i,j)处的的像素值,以此类推。
假如目标图的象素坐标为(1,1),那么反推得到的对应于源图的坐标是(0.75,0.75), 这其实只是一个概念上的虚拟象素,实际在源图中并不存在这样一个象素,那么目标图的象素(1,1)的取值不能够由这个虚拟象素来决定,而只能由源图的这四个象素共同决定:(0,0)(0,1)(1,0)(1,1),而由于(0.75,0.75)离(1,1)要更近一些,那么(1,1)所起的决定作用更大一些,这从公式1中的系数uv=0.75×0.75就可以体现出来,而(0.75,0.75)离(0,0)最远,所以(0,0)所起的决定作用就要小一些,公式中系数为(1-u)(1-v)=0.25×0.25也体现出了这一特点。算法步骤详述:
假设原始图像大小为size=m×n,其中m与n分别是原始图像的行数与列数。若图像的缩放因子是t(t>0),则目标图像的大小size=t×m×t×n。对于目标图像的某个像素点P(x,y)通过P*1/t可得到对应的原始图像坐标P’( x1,y1),其中x1=x/t,y1=y/t,由于x1,y1都不是整数所以并不存在这样的点,这样可以找出与它相邻的四个点的灰度f1、f2、f3、f4,使用双线性插值算法就可以得到这个像素点P’(x1,y1)的灰度,也就是像素点P(x,y)的灰度。
一个完整的双线性插值算法可描述如下:
- 通过原始图像和比例因子得到新图像的大小,并创建新图像。
- 由新图像的某个像素(x,y)映射到原始图像(x’,y’)处。
- 对x’,y’取整得到(xx,yy)并得到(xx,yy)、(xx+1,yy)、(xx,yy+1)和(xx+1,yy+1)的值。
- 利用双线性插值得到像素点(x,y)的值并写回新图像。
- 重复步骤2直到新图像的所有像素写完。