赫夫曼树

赫夫曼树：权值越大的结点离根结点越近的二叉树就是最优二叉树。 WPL值也越小。

WPL值：权值乘根结点到自己的线数。

权值：这个9就是权值。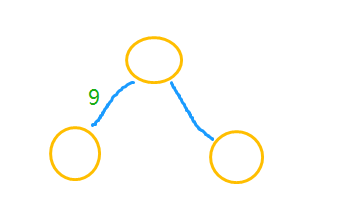

图中的b就是赫夫曼树。

怎么形成一个赫夫曼树呢？

假如有这么一个数组：3，7，19，8，30，1

形成的思路是：先进行排序。然后把最小的两个生成一个二叉树。根节点是这两个权值的和。然后把最小的这两个删除掉。把生成的那个根节点放到数组中。然后再进行排序。再挑选出最小的两个。

排序：1  3  7  8  19  30

排序：4   7  8  19  29  30

排序：8  11  19  29  30

排序：19  19  29  30

排序：29   30   38

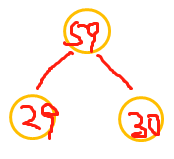
排序：38   59

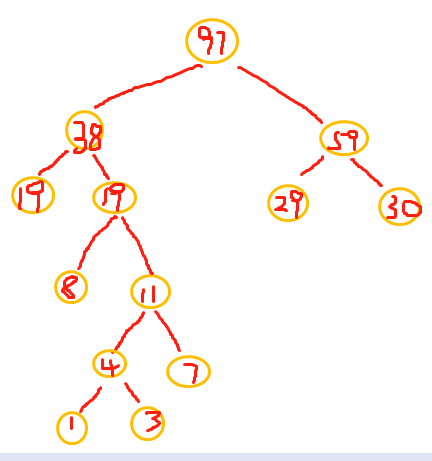
这就是生成赫夫曼树的原理。

接下来我们用代码来实现一下：

package com.Huffman;

/**
 * 链表。赫夫曼树结构用到的双链表。
 */
public class Node implements Comparable<Node> {
    //数据
    int value;
    //左儿子
    Node leftNode;
    //右儿子
    Node rightNode;

    public Node(int value) {
        this.value = value;
    }


    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }

    //排序。前面加 - ，是倒序。
    @Override
    public int compareTo(Node o) {
        return -(this.value-o.value);
    }
}

package com.Huffman;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

/**
 * 赫夫曼树：就是最优二叉树。权值越大的结点离根结点越近的二叉树。WPL值最小。
 */
public class HuffmanTree {
    public static void main(String[] args) {
        int arr[] = {3, 7, 8, 29, 5, 11, 23, 14};
        Node node = createHuffmanTree(arr);
        System.out.println(node);
    }
    //创建赫夫曼树。
    public static Node createHuffmanTree(int[] arr){
        //先使用数组中的所有元素。创建若干个二叉树。（只有一个节点）
        List<Node> nodes = new ArrayList<>();
        for (int value : arr) {
            nodes.add(new Node(value));
        }
        //循环处理.要不断的两个相加。然后删除。最后只剩下一个。
        while(nodes.size()>1){
            // 排序
            Collections.sort(nodes);
            //取出权值最小的两个二叉树（左和右）。
            Node left = nodes.get(nodes.size() - 1);
            Node right = nodes.get(nodes.size() - 2);
            //构建一个新的二叉树。
            Node newTree = new Node(left.value + right.value);
            //把取出的那两个删除掉。
            nodes.remove(left);
            nodes.remove(right);
            //放在原来的二叉树集合中。
            nodes.add(newTree);

        }
        return nodes.get(0);
    }
}