浅谈神经网络算法

我们在设计机器学习系统时，特别希望能够建立类似人脑的一种机制。神经网络就是其中一种。但是考虑到实际情况，一般的神经网络（BP网络）不需要设计的那么复杂，不需要包含反馈和递归。
人工智能的一大重要应用，是分类问题。本文通过分类的例子，来介绍神经网络。

1.最简单的线性分类

一个最简单的分类，是在平面上画一条直线，左边为类0，右边为类1，直线表示为(z=ax+by+c)
这是一个分类器，输入(x,y)，那么，要求的参数有三个:a,b,c。另外注意c的作用，如果没有c，这条直线一定会过原点。

因此，我们可以设计一个简单的神经网络，包含两层，输入层有三个节点，代表x,y,1，三条线分别代表a,b,cg(z)对传入的值x进行判别，并输出结果。

[z=θ_0+θ_1X_1+θ_2X_2 ]

但是，由于z的值可能为[(-infty,+infty)],为了方便处理，需要将其压缩到一个合理的范围，还需sigmoid函数:

[a(z)=frac{1}{1-e^{-z}} ]

这样的激励函数，能够将刚才的区间，压缩到([0,1])。
至于如何训练，会在之后的章节中讲解。

2.多层级神经网络

刚才展示了最简单的二分类，如果有四个分类，那一条线就无法满足要求了。想象两条直线，就会将平面划分为四个区域，一个三角区域相当于两个子平面求交集。
因此直觉告诉我们，如果有多个神经元，那么这样的问题能表现为问题的“逻辑与”操作。将第一节中介绍的神经网络的输出，再做一个判断层，即多层网络。

但是，如何实现逻辑与呢？用下面的图一目了然：

仔细看下，这相当于创建一条线，除非(x_1)和(x_2)都等于1，否则(h_ heta(x)<0)。
进一步地，如果我们能够对区域求并集，那么总可以对不同的子区域求并。而实现并操作和与操作是类似的：

此处就能看到sigmoid函数的作用了，如果没有它对数值的放缩，并和与的操作就无法实现了。
输出还能作为下一级的输入，从而增加了一个隐层，产生了单隐层神经网络，再复杂一些，如果网络层数特别多，则叫做深度学习网络，简称深度学习。

之前针对一个线性不可分的区域，需要将其变换到更高维度的空间去处理。但如果用神经网络，你总可以通过n条直线，将整个区间围起来。只要直线数量够多，总能绘制出任意复杂的区域。每一个子区域都是凸域：

简直不能更酷！下面这张图总结了不同类型的神经网络具备的功能：

数学家证明了，双隐层神经网络能够解决任意复杂的分类问题。但我们的问题到此为止了吗？不见得！
这里还有几个问题：

• 异或如何实现？异或肯定是不能通过一条直线区分的，因此单层网络无法实现异或，但两层（包含一个隐层）就可以了。
• 过拟合问题：过多的隐层节点，可能会将训练集里的点全部围进去，这样系统就没有扩展性了。如何防止过拟合？
• 如何训练：如何计算出合理的神经网络参数？（隐层节点数）

3.如何训练神经网络

如果一个平面，有6个点，分成三类。如何设计呢？

一种最狂暴的方法，是对每一个点都用四条线围起来，之后，再对六个区域两两取并集。形成下面这张超复杂的图：

解释一下为什么要有这么多个节点：
第一层：x,y再加bias,三个
第二层：每个点需要四条线围起来，加上bias，总共4*6+1=25个
第三层：一个节点处于该类的条件是在四条线的中间（交集），因此每四个点汇成一个点，24/4+1=7个
第四层：三分类问题，需要对每两个区域求并集，因此需要6/2+1=4个

但这样的解法，使用了3+25+7+4=39个节点，需要111个参数。这样的系统非常复杂，对未知节点几乎没有任何扩展性。
仔细思考这个问题， 我们能够通过更少的节点和层数，来简化这个问题嘛？只要三条直线就可以！节点数量大大减少。不仅训练效率更高，而且可扩展能力很强。对更复杂的例子，我们又不是神仙，怎么知道设计几个隐层和多少个节点呢？
所谓超参数，就是模型之外的参数，在这个例子中，就是隐层的数量和节点的数量。通常来说，线性分类器（回归）只需要两层即可，对于一般的分类问题，三层足够。
一个三层的神经网络，输入和输出节点的数量已经确定，那如何确定中间层（隐层）的节点数量呢？一般有几个经验：

• 隐层节点数量一定要小于N-1(N为样本数)
• 训练样本数应当是连接权（输入到第一隐层的权值数目+第一隐层到第二隐层的权值数目+...第N隐层到输出层的权值数目，不就是边的数量么）的2-10倍（也有讲5-10倍的），另外，最好将样本进行分组，对模型训练多次，也比一次性全部送入训练强很多。
• 节点数量尽可能少，简单的网络泛化能力往往更强
• 确定隐层节点的下限和上限，依次遍历，找到收敛速度较快，且性能较高的节点数

如何表示一个神经网络？网络有m层，每层的节点分别为(node_0,node_1...node_m)，节点最多的层，有m个节点，那么我们可以将其表达为一个矩阵W,规模为(m*n)，内部有些值是没有定义的。

4.训练算法

线性可分

如果输入和输出是线性关系（或者是正相关），那么想象我们在调节一个参数时，当输出过大，那就把输入调小一些，反之调大一些，最后当输出和我们想要的非常接近时，训练结束。这个就好比，在平面上，如果一个点被分配到了错误的输出，就应该对直线平移和扭转，减少该直线到这个点的距离，从而实现重新分区。
进一步地，如果向量的多个分量互相独立，那么方法也和上面的类似(x_1=>y_1,x_2=>y_2)，分别调节(x_1)和(x_2)的参数，最终让结果接近，训练结束。

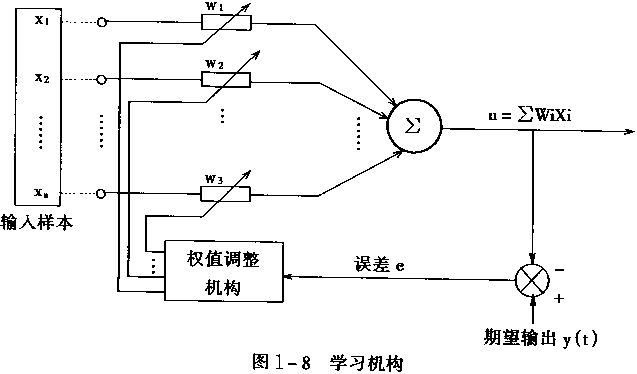
而一个感知器结构可表示如下：

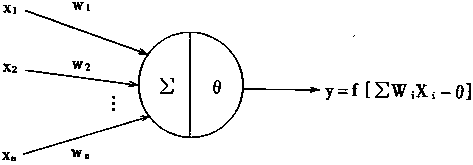
反思上面的过程，我们实际上是在衡量误差，根据误差来修改权重。

线性不可分

如果输入和输出的关系比较复杂，如二次函数(y=x^2)，那当超过x=0的位置之后，反而成了递增了，此时一个线性的判断函数就不起作用了。因此，上面的方法，不能推广到所有的前馈网络中。
怎么办？那就只能使用梯度(LMS)法了。
梯度法，是对于样本集(X_1,X_2..X_n)，找到一个(W^*),使得(f(W^* dot X_i) X_i)与输出(Y_i)尽可能接近，其中(f)是激励函数。误差表示为：

[e= frac{1}{2}sum_{i=1}^{n}{(Y_i-Y_i^*)}^{2} ]

为了能够调节误差e,使之尽可能小，则需要求其导数，发现其下降的方向：

[grad_w e= frac{partial e}{partial W} = sum_{k=1}^{n}frac{partial e_k}{partial W} ]

其中:

[e_k=frac{1}{2} {(Y_k-Y^-_k)}^2 ]

对偏导进行求解：

每次迭代的计算公式为：

最终：

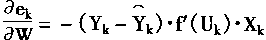
其几何意义就是，误差的偏导，等于在(X_k)位置上的值，乘以误差，再乘以激励函数的偏导。
所以，每次的权重矩阵(W)的修改，应当通过求误差的偏导（梯度）来实现。比之前的直接通过误差来调整，具备更好的适应性。
但是，这样的梯度法，对于实际学习来说，效率还是太慢，我们需要更快的收敛方法。

BP算法

BP算法就是所谓的反向传播算法，它将误差进行反向传播，从而获取更高的学习效率。这很像烽火台，如果前线战败了，那么消息就通过烽火台传递回指挥部，指挥部去反思问题，最终改变策略。
但这带来一个问题，中间层的误差怎么计算？我们能简单地将权重和残差的乘积，返回给上一层节点（这种想法真暴力，从左到右和从右到左是一样的）。

这相当于三次传播：

-第一步：从前向后传播FP
-第二步：得到值z，误差为y,将误差反向传播，获得每个节点的偏差$sigma$
-第三步：再次正向传播，通过上一步的$sigma$，再乘以步长，修改每一个神经元突触的权重。

下面一张图展示了完整的BP算法的过程，我看了不下20遍：

更有趣的是，sigmoid求导之后，特别像高斯（正态）分布，而且sigmoid求导非常容易。

5.总结

这样的一篇文章真是够长了，原本还想再介绍一个神经网络的Python实现，可是考虑到篇幅的限制，最终作罢。在下一期继续介绍如何实现BP神经网络和RNN（递归神经网络）。