一堆递推题

目录

• 一堆递推题
  • P1367【训练题】爬楼梯[2]
    • 描述
    • 輸入
    • 輸出
    • 輸入範例 1
    • 輸出範例 1
    • 提示
    • 思路
  • 铺瓷砖
    • 描述
    • 輸入
    • 輸出
    • 輸入範例 1
    • 輸出範例 1
    • 思路
  • 城市路径
    • 描述
    • 輸入
    • 輸出
    • 輸入範例 1
    • 輸出範例 1
    • 提示
    • 思路
  • 彩带
    • 描述
    • 輸入
    • 輸出
    • 輸入範例 1
    • 輸出範例 1
    • 提示
    • 思路
  • 斐波那契前N项和
    • 描述
    • 輸入
    • 輸出
    • 輸入範例 1
    • 輸出範例 1
    • 提示
    • 思路
  • 偶数个3
    • 描述
    • 輸入
    • 輸出
    • 輸入範例 1
    • 輸出範例 1
    • 思路
  • 回文拆分
    • 描述
    • 輸入
    • 輸出
    • 輸入範例 1
    • 輸出範例 1
    • 思路

一堆递推题

同步：<https://buringstraw.win/index.php/archives/27/ >

——来自义冢OJ和义冢OJ的contests

P1367【训练题】爬楼梯[2]

描述

　　何老师爬楼梯，他可以每步上 1 、2或3 级，输入楼梯的级数，求不同的走法数。例如：楼梯一共有3级，他可以每步都走一级，或者第一步走一级，第二步走两级，也可以第一步走两级，第二步走一级，还有就是第一步就上3级，所以一共4种方法。

　　但不幸的是，楼梯上有K级坏了，何老师不能踩在这些楼梯上，现在给出楼梯的级数N和坏了的K级楼梯，请你计算他上楼梯的方法总数。

輸入

　　第一行：N、K。　　第二行：K个整数h[i]，表示坏了的楼梯的级数(1<=h[i]<=N)。

輸出

　　不同的走法数，这个数字可能很巨大，所以输出最后答案mod 1234567。

輸入範例 1

5 2
2 4

輸出範例 1

2

提示

　　1 <= N <= 1000 0 <= k < N

思路

把所有有坑的楼梯的方案数在递推过程中设为0

注意有可能最前面几级也有坑

所以用0作为边界

中途检查是否越界

#include<cstdio>
#include<iostream>
using namespace std;

const int MAXN=1005;

int f[MAXN];
bool h[MAXN];

int main(){
	int n,k;
	cin>>n>>k;
	for(int i=1;i<=k;++i){
		int t;
		cin>>t;
		h[t]=1;
	}
	f[0]=1;
//	f[1]=1;
	for(int i=1;i<=n;++i){
		if(h[i]){
			f[i]=0;
			continue;
		}
		else if(!f[i]){
			if(i-1>=0)f[i]+=f[i-1];
			if(i-2>=0)f[i]+=f[i-2];
			if(i-3>=0)f[i]+=f[i-3];
			f[i]%=1234567;
		}
	}
	cout<<f[n]<<endl;
	return 0;
}

铺瓷砖

描述

用红色的 1×1 和黑色的 2×2 两种规格的瓷砖不重叠地铺满 n×3 的路面，求出有多少种不同的铺设方案。

輸入

一行一个整数 n，0<n<1000。

輸出

一行一个整数，为铺设方案的数量模12345的结果。

輸入範例 1

2

輸出範例 1

3

思路

从之前一格开始填有一种方法

从之前两格开始填有3种方法

但是全用1x1包含在从之前一格开始填里面

所以f[i]=f[i-1]+f[i-2]*2

f[0]=f[1]=1;

#include<cstdio>
#include<iostream>
using namespace std;

int f[1005];

int main(){
	int n;
	cin>>n;
	f[0]=f[1]=1;
	//f[2]=3;
	for(int i=2;i<=n;++i){
		f[i]=f[i-1]+f[i-2]*2;
		f[i]%=12345;
	}
	cout<<f[n]<<endl;
	return 0;
}

城市路径

描述

地图上有 n 个城市，一只奶牛要从 1 号城市开始依次经过这些城市，最终到达 n 号城市。但是这只奶牛觉得这样太无聊了，所以它决定跳过其中的一个城市(但是不能跳过 1 号和 n 号城市)，使得它从 1 号城市开始，到达 n 号城市所经过的总距离最小。假设每一个城市 i 都有一个坐标(x i ，y i )，从 (x 1 ，y 1 ) 的城市 1 到 (x 2 ，y 2 ) 的城市 2 之间的距离为 | x 1 -x 2 | + | y 1 -y 2 | 。

輸入

第 1 行 1 个正整数 n，表示城市个数。接下来的 n 行，每行 2 个数 x i 和 y i ，表示城市 i 的坐标。

輸出

一行一个数，使得它从1号城市开始，跳过某一个城市，到达n号城市所经过的最小总距离。

輸入範例 1

4
0 0
8 3
11 -1
10 0

輸出範例 1

14

提示

【样例说明】跳过 2 号城市。【数据规模】对于 40% 的数据满足：n≤1000。对于 100% 的数据满足：3≤n≤100000，-1000≤x i ，y i ≤1000。

思路

有的题，表面上是一道递推题，实际上可以用模拟做
​ ——鲁迅

这是贪心

​ ——hqxperisino大佬

比较每一个点删除之后对路程的影响，选出删除之后最短的

#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;

const int MAXN=1e5+5;

struct zb{
	int x,y;
} city[MAXN];
int n;

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		scanf("%d%d",&city[i].x,&city[i].y);
	}
	int maxs=0,maxi=0;
	int he=0;
	
	for(int i=2;i<n;++i){
		int tmp=
			abs(city[i+1].x-city[i].x)+abs(city[i+1].y-city[i].y)
			+abs(city[i-1].x-city[i].x)+abs(city[i-1].y-city[i].y);
		tmp-=abs(city[i+1].x-city[i-1].x)+abs(city[i+1].y-city[i-1].y);
		if(tmp>maxs){
			maxi=i;
			maxs=tmp;
		}
		he+=abs(city[i-1].x-city[i].x)+abs(city[i-1].y-city[i].y);
	}
	he+=abs(city[n-1].x-city[n].x)+abs(city[n-1].y-city[n].y);
	he-=maxs;
	printf("%d
",he);
	return 0;
}

彩带

描述

一中 90 周年校庆，小林准备用一些白色、蓝色和红色的彩带来装饰学校超市的橱窗，他希望满足以下两个条件：

(1) 相同颜色的彩带不能放在相邻的位置；

(2) 一条蓝色的彩带必须放在一条白色的彩带和一条红色的彩带中间。

现在，他想知道满足要求的放置彩带的方案数有多少种。

例如，如图 9.4-1 所示为橱窗宽度n=3 的所有放置方案，共 4 种。

輸入

一行一个整数 n，表示橱窗宽度(或者说彩带数目)。

輸出

一行一个整数，表示装饰橱窗的彩带放置方案数。

輸入範例 1

3

輸出範例 1

4

提示

对 30% 的数据满足：1≤n≤15。对 100% 的数据满足：1≤n≤45。

思路

此题感谢perisino大佬的指点

f[i]为彩带数目为i时的方案数

注意最后一条不能是蓝色

当

• 第(i-1)条为红色或白色：因为最后一条不能是蓝色，所以有一种情况

• 第(i-1)条为蓝色：第i条与第(i-2)条颜色相反，有一种情况

• 大佬之前把第二个(i-1)写成了(i-2)我差点没看懂

所以f[i]=f[i-1]+f[i-2]

#include<cstdio>
#include<iostream>
using namespace std;

const int MAXN=50;

int f[MAXN];
int n;

int main(){
	f[1]=2;
	f[2]=2;
	cin>>n;
	for(int i=3;i<=n;++i){
		f[i]=f[i-1]+f[i-2];
	}
	cout<<f[n]<<endl;
	return 0;
}

斐波那契前N项和

描述

求斐波那契数列前n项和取模m

輸入

一行两个整数n m

輸出

输出前n项和取模m

輸入範例 1

5 1000

輸出範例 1

12

提示

1<=n<=2*10^91<=m<=1000000010

思路

是前n项和不是第n项

数据范围非常大，用矩阵

矩阵快速幂都忘了，丢人

矩阵A：1x3

​ 内容：f(i-1),f(i-2),g(i-1)

​ 其中f(i)表示斐波那契数列的第i项，g(i)表示前i项的和

矩阵B：3x3

​ 内容：

		1 1 1
		1 0 1
		0 0 1

则 (f(n)=Acdot B^{(n-2)})

要用long long要用long long要用long long

#include<cstdio>
#include<cstring>
#include<iostream>
#define LL long long
using namespace std;

const LL MAXN=5;

LL n,m;

struct juzhen{
	private:
		LL v[MAXN][MAXN];
		LL h,l;
		
		void prLL(void){
			for(LL i=1;i<=h;++i){
				for(LL j=1;j<=l;++j){
					cout<<v[i][j]<<' ';
				}
				cout<<'
';
			}
		}
	
	public:
		juzhen(LL he,LL le){
			memset(v,0,sizeof(v));
			h=he,l=le;
		}
		
		friend juzhen operator *(juzhen a,juzhen b){
			juzhen c(a.h,b.l);
			for(LL i=1;i<=a.h;++i){
				for(LL j=1;j<=b.l;++j){
					 for(LL k=1;k<=a.l;++k){
					 	c.v[i][j]+=(a.v[i][k]*b.v[k][j]%m);
					 	c.v[i][j]%=m;
					 }
				}
			}
			return c;
		}
		
		friend juzhen operator ^(juzhen a,LL b){
			
			juzhen ret(a.h,a.l),sum=a;
			for(LL i=1;i<=a.h;++i){
				ret.v[i][i]=1;
			}
			while(b){
				if(b&1){
					ret=ret*sum;
				}
				sum=sum*sum;
				b>>=1;
			}
//			ret.prLL();
			return ret;
		}
		
		void writeV(LL x,LL y,LL val) {
			v[x][y]=val;
		}
		
		LL callV(LL x,LL y){
			return v[x][y];
		}
};

	juzhen a(1,3),b(3,3);
int main(void){
	cin>>n>>m;
	a.writeV(1,1,1);
	a.writeV(1,2,1);
	a.writeV(1,3,2);
	
	b.writeV(1,1,1);
	b.writeV(1,2,1);
	b.writeV(1,3,1);
	b.writeV(2,1,1);
	b.writeV(2,2,0);
	b.writeV(2,3,1);
	b.writeV(3,1,0);
	b.writeV(3,2,0);
	b.writeV(3,3,1);
	
	juzhen c=a*(b^(n-2));
	cout<<c.callV(1,3)<<endl;
	
	
	return 0;
}

偶数个3

描述

编程求出所有的 n 位数中，有多少个数中有偶数个数字 3。

輸入

一行一个正整数 n，0<n<1000。

輸出

一行一个正整数，表示 n 位数中有多少个数有偶数个 3。最后答案为12345取模

輸入範例 1

2

輸出範例 1

73

思路

好难一道题！

看着大佬打完表找出规律AC了，我的眼眶也湿润了。

然后我也dfs打了个表

然而找不到半分规律

最后看了大佬的规律和题解。。。

发现这规律可能我这辈子都找不出来。。

可能这就是我和大佬的差距吧

这里的大佬指的是(wyx大佬)[https://wuyanxi.top]和(perisino大佬)[https://cnblogs.com/perisino]

忽略上面这部分

主要解法就是用f[i][0]表示i位数中有偶数个3的数量

​ 用f[i][1]表示i位数中有奇数个3的数量

若一个(i-1)位数中有偶数个3，要使i位数有偶数个3

则可以在其后追加1,2,4,5,6,7,8,9,0

若有奇数个，则可追加一个3

可得

f[i][0]=f[i-1][0]*9+f[i-1][1];
f[i][1]=f[i-1][1]*9+f[i-1][0];

回文拆分

描述

对一个正整数K，求出K的所有拆分，并统计输出其中回文数列的个数。 所谓回文数列是指该数列中的所有数字，从左向右或从右向左看都相同。 例如：

K=4时，有如下的拆分：

4=1+1+1+1 （回文数列1）

=1+1+2

=1+2+1 （回文数列2）

=2+1+1

=2+2 （回文数列3）

=1+3

=3+1

回文数列共有3个

輸入

一行，一个正整数K，1<=K<=26

輸出

一个正整数，表示回文数列个数

輸入範例 1

4

輸出範例 1

3

思路

有的题在递推的contest里，但它实际上是道递归题

​ ——鲁迅

写了个dfs想看看能过几个点，没想到AC了。

#include<cstdio>
#include<iostream>
using namespace std;

int f[30];

void dfs(int step,int tot);
int k,cnt;

int main(){
	cin>>k;
	dfs(1,0);
	cout<<cnt<<endl;
	return 0;
}

void dfs(int step,int tot){
	if(tot>k)return;
	if(tot==k){
		bool flag=1;
		for(int i=1;i<=(step-1)/2;++i){
			if(f[i]!=f[step-i]){
				flag=0;
				break;
			}
		}
		if(flag){
			++cnt;
//			for(int i=1;i<step;++i){
//				cout<<f[i]<<' ';
//			}
//			cout<<'
';
		}
	}
	for(int i=1;i<=k-tot&&i<k;++i){
		f[step]=i;
		dfs(step+1,tot+i);
	}
}

看到自己是400+ms，而其他人都是2,3ms，感觉很尴尬

就打了个表

for(int i=1;i<=26;++i){
    cnt=0;
    memset(f,0,sizeof(f));
    k=i;
    dfs(1,0);
    cout<<i<<' '<<cnt<<endl;
}

得到

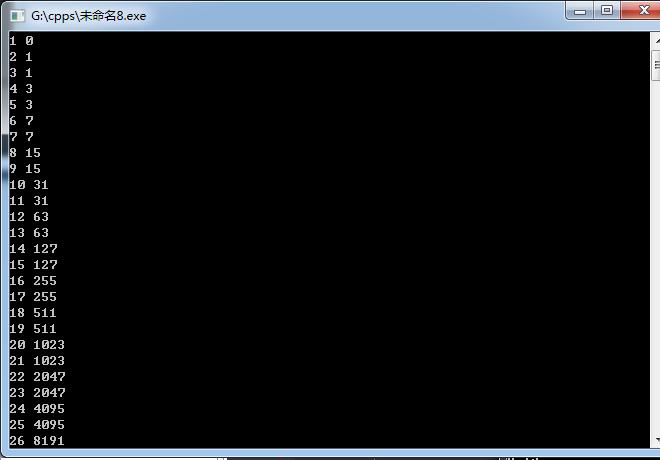
这不是((2^n-1))吗。。。

所以又AC一遍

#include<cstdio>
#include<iostream>
using namespace std;

int qkpow(int x,int y);

int main(void){
	int k;
	cin>>k;
	cout<<qkpow(2,k/2)-1<<endl;
	return 0;
}

int qkpow(int x,int y){
	if(y==0){
		return 1;
	}
	int ret=1,sum=x;
	while(y){
		if(y&1){
			ret*=sum;
		}
		sum*=sum;
		y>>=1;
	}
	return ret;
}

恩~~

然后去找了找正解

每个数必须被分成3部分。

以4为例：4=1+2+1，我们发现中间的数字只能是偶数，即2和0，为2的时候有1种数列，0的时候有2种数列。

再来研究一下6，当为4的时候有1种，为2的时候有2种，为0的时候有4种。

最后看一下5，情况和4非常的相似，只是中间的数字只能是奇数。

就是令f[i]为i的拆分可能的情况，如果i为奇数，f[i]=f[i-1]，i为偶数，f[i]=f[i-1]*2

哇，%%%