P4128 [SHOI2006]有色图
题目描述
如果一张无向完全图(完全图就是任意两个不同的顶点之间有且仅有一条边相连)的每条边都被染成了一种颜色,我们就称这种图为有色图。如果两张有色图有相同数量的顶点,而且经过某种顶点编号的重排,能够使得两张图对应的边的颜色是一样的,我们就称这两张有色图是同构的。以下两张图就是同构的,因为假如你把第一张图的顶点((1,2,3,4))置换成第二张图的((4,3,2,1)),就会发现它们是一样的。
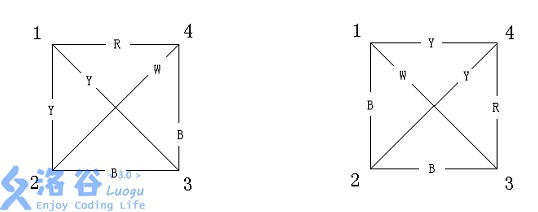
你的任务是,对于计算所有顶点数为(n),颜色种类不超过(m)的图,最多有几张是两两不同构的图。由于最后的答案会很大,你只要输出结论模(p)的余数就可以了((p)是一个质数)
输入输出格式
输入格式:
输入文件只有一行,由三个正整数(n,m,p)组成,他们满足(1≤n≤53),(1≤m≤1000),(n<p≤10^9)
输出格式:
即总数模(p)后的余数
我们发现(polya)处理的是点的置换,现在要处理边的,怎么办呢?
其实是一样的,我们发现每个点的置换都可以对应一个边的置换,边的置换同样构成了一个群,注意这个群的大小和点的置换组成的群的大小是一样的。
然后我们枚举本质不同的点的置换,这个本质不同是按轮换大小的集合定义的,相当于对(n)进行和式拆分,相当于(n=L_1+L_2+dots+L_p),(L)是每个轮换的大小,这个状态量是比较小的。
注意搜的时候为了避免重复,需要(L_1le L_2le dots L_p)这样搜
这时候就可以通过点的置换求出边的置换的轮换大小的信息了。
分类讨论
- 当两个点处于两个不同轮换(L_i)和(L_j)中时,产生的边的轮换的大小为$frac{L_i,L_j}{lcm(L_i,L_j)}=gcd(i,j) $,就是考虑两个点一起转,然后要转公倍数那么长才回来
- 当两个点处于同一轮换(L_i)中时
- 当(L_i)为奇数,轮换个数为(frac{L_i*(L_i-1)}{2*L_i}=frac{L_i-1}{2}),每个轮换长度为(L_i)
- 当(L_i)为偶数,轮换个数为(frac{frac{L_i(L_i-1)}{2}-frac{L_i}{2}}{L}+1=frac{L_i}{2}),这里有一个轮换长度为(frac{L_i}{2}),是相差长度等于(frac{L_2}{2})的点组成的边所在的集合。
然后统计所有轮换的贡献(C=sumlfloorfrac{L_1}{2} floor+sumsum gcd(L_i,L_j))
再统计一下枚举的(L)的总情况,为(D=frac{n!}{prod_{i=1}^pL_iprod_{i=1}^kB_i}),其中(B_i)为(sum_{j=1}^p[L_j=i]),这点除(L_i)是每种情况都是一个圆排列,除(B_i)是每个同样大小的圆排列是无标号的。
答案是(frac{sum Dm^C}{n!})
#include <cstdio>
int ans,L[60],fac[60],n,m,mod,cnt;
#define mul(a,b) (1ll*(a)*(b)%mod)
#define add(a,b) ((a+b)%mod)
int gcd(int a,int b){return b?gcd(b,a%b):a;}
int qp(int d,int k){int f=1;while(k){if(k&1)f=mul(f,d);d=mul(d,d),k>>=1;}return f;}
void cal()
{
int C=0,S=1;
for(int i=1;i<=cnt;i++)
C=add(C,L[i]/2);
for(int i=1;i<=cnt;i++)
for(int j=i+1;j<=cnt;j++)
C=add(C,gcd(L[i],L[j]));
int B=1;
for(int i=1;i<=cnt;i++)
{
if(L[i]!=L[i-1])
{
S=mul(S,fac[B]);
B=0;
}
++B;
S=mul(S,L[i]);
}
S=mul(S,fac[B]);
S=qp(S,mod-2);
C=qp(m,C);
ans=add(ans,mul(S,C));
}
void dfs(int res,int lim)
{
if(!res) cal();
for(int i=lim;i<=res;i++)
{
L[++cnt]=i;
dfs(res-i,i);
--cnt;
}
}
int main()
{
scanf("%d%d%d",&n,&m,&mod);
fac[0]=1;
for(int i=1;i<=n;i++) fac[i]=mul(fac[i-1],i);
dfs(n,1);
printf("%d
",ans);
return 0;
}
2018.12.22