P1282 多米诺骨牌 DP

　　

题目描述

多米诺骨牌有上下2个方块组成，每个方块中有1~6个点。现有排成行的

上方块中点数之和记为S1，下方块中点数之和记为S2，它们的差为|S1-S2|。例如在图8-1中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。

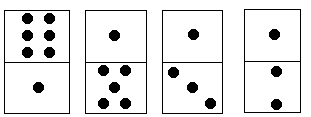
对于图中的例子，只要将最后一个多米诺骨牌旋转180°，可使上下2行点数之差为0。

输入输出格式

输入格式：

输入文件的第一行是一个正整数n(1≤n≤1000)，表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数a和b，且1≤a，b≤6。

输出格式：

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

输入输出样例

输入样例#1： 复制

4
6 1
1 5
1 3
1 2

输出样例#1： 复制

1


可以将其抽象为背包问题   
背包问题的核心就是：多放入一个物件对决策的影响
要求什么dp什么
所有dp【i】【j】就是前i个物品 为j点数的最小翻转次数
要求点数最小  那么就从j 0-MAXN取值即可

#include<bits/stdc++.h>
using namespace std;
//input
#define rep(i,x,y) for(int i=(x);i<=(y);++i)
#define RI(n) scanf("%d",&(n))
#define RII(n,m) scanf("%d%d",&n,&m);
#define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k)
#define RS(s) scanf("%s",s)
#define LL long long
#define REP(i,N)  for(int i=0;i<(N);i++)
#define CLR(A,v)  memset(A,v,sizeof A)
//////////////////////////////////
#define N 8000
#define inf -0x3f3f3f3f
int dp[1005][2*N+5];

int main()
{
  int n;
  RI(n);
  CLR(dp,0x7f);
  dp[0][N]=0;
  int a,b;
  rep(i,1,n)
  {
      RII(a,b);
      int dis=a-b;
      for(int j=-6000;j<=6000;j++)
      {
          dp[i][j+N]=min(dp[i-1][j-dis+N],dp[i-1][j+dis+N]+1);
      }
  }
  rep(i,0,N-1)
  {
      if(dp[n][i+N]<=1000)
          cout<<dp[n][N+i];break;
      if(dp[n][N-i]<=1000)
          cout<<dp[n][N-i];break;
  }
}