人类史上最大最好的希望事件

作为CNCS的半壁江山，狗哥常常在宇宙中心邵阳眺望黄浦江，夜晚的星空总是迷人，有时候还能见到彗星滑落。

狗哥是幸运的，他在两秒钟内看到了十七颗彗星划过天际，作为打ACM的学者，自然不会有「稳定-1」情况。他开始研究彗星运动的轨迹，发现他们都遵照斐波那契螺旋线在运动着。

尤里卡！狗哥觉得这就是找寻「生命，宇宙和一切的终极答案」的精要所在，但是怎么表示呢？狗哥觉得求取斐波那契螺旋线经过的一个个方格的面积之和就是公式的表现。

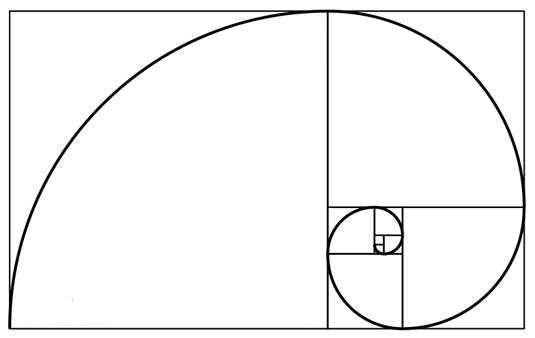
例如下图，螺旋线每划过一个方格，都转过了四分之一圈。如果我们以四分之一圈为单位，那么我们用类似带分数的形式表示螺旋线转动的起点和终点。例如，0+0 到 0 + 1 意即从第一个方格转到第二个方格，划过了前两个方格，他们的面积之和为2（1+1）。同理，0+0 到 1+0 划过了前五个方格，他们的面积之和为40（1+1+4+9+25）。

但是聪明的狗哥需要一个程序去获得指定范围内的螺旋线面积之和，狗哥给了你一首「希望之花」的时间，而他需要利用这个时间去打出四暗刻单骑。如果你能完成这个程序，狗哥会封你为格拉摩根伯爵

 

Input

不定组数据。

首先输入一个整数Q，代表狗哥询问次数。

接下来Q行，每行四个整数a,b,c,d，代表狗哥想求 a+b 到 c+d 之间的螺旋线面积之和。

1<= Q <= 10000

0<= a,c <= 10000

0 <= b,d <= 3

结果对192600817取模。

 

Output

一个数字，表示螺旋线面积之和。

 

Sample Input

4 0 0 0 1 0 0 1 0 1 2 2 1 1 1 0 3 4 0 0 0 1 0 0 1 0 1 2 2 1 1 1 0 3

 

Sample Output

2 40 4791 98 2 40 4791 98

求的是斐波那契数列平方和  ：

有如下数学公式 ：   斐波那契 1-n个的平方和等于 f[n]*f[n+1]

用矩阵快速幂来加速计算斐波那契数列

因为已经到9位了   数据类型要开longlong  还有就是N是50000 比赛就因为这个死活wa

#include<bits/stdc++.h>
using namespace std;
//input by bxd
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define RI(n) scanf("%d",&(n))
#define RII(n,m) scanf("%d%d",&n,&m)
#define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k)
#define RS(s) scanf("%s",s);
#define LL long long
#define REP(i,N)  for(int i=0;i<(N);i++)
#define CLR(A,v)  memset(A,v,sizeof A)
//////////////////////////////////
#define N 50000
#define mod 192600817
struct mp
{
    long long m[2][2];
}ans,base;

mp mul(mp a,mp b)
{
    mp temp;
    rep(i,0,1)
    rep(j,0,1)
    {
        temp.m[i][j]=0;
        rep(k,0,1)
        temp.m[i][j]=(temp.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
    }
    return temp;
}

long long fast(mp a,int n)
{
    CLR(ans.m,0);
    rep(i,0,1)
    ans.m[i][i]=1;
    while(n)
    {
        if(n&1)
            ans=mul(ans,a);
        a=mul(a,a);
        n>>=1;
    }
    return ans.m[0][1]%192600817;
}

int main()
{
    int q;
    while(RI(q)==1)
    {
        while(q--)
        {
            int a,b,c,d;
            RIII(a,b,c);RI(d);
            int c1=a*4+b;
            int c2=c*4+d;
            if(c1>c2)swap(c1,c2);
            c2++;
            base.m[0][0]=base.m[1][0]=base.m[0][1]=1;
            base.m[1][1]=0;
            long long ans1=fast(base,c1)*fast(base,c1+1)%mod;
            long long ans2=fast(base,c2)*fast(base,c2+1)%mod;
            printf("%lld
",(ans2-ans1+mod)%mod );
        }
    }
}

还有一种方法是前缀和  更加有普遍性

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N=4e4+100;
ll m[N];
ll f[N];
int main()
{
    m[1]=1;
    f[1]=1;
    for(ll i=2;i<=4e4+50;i++){
        f[i]=(f[i-1]+f[i-2])%192600817;
        m[i]=(f[i]*f[i])%192600817;
    //cout<<m[i]<<endl;
        m[i]=m[i]+m[i-1];
        //cout<<m[i]<<endl;

    }
    int n,a,b,c,d;
    while(~scanf("%d",&n)){
        while(n--){
            scanf("%d%d%d%d",&a,&b,&c,&d);
            a=a*4+b+1;c=c*4+d+1;
            if(a>c) swap(a,c);
            printf("%I64d
",(m[c]-m[a-1])%192600817);
        }
    }
    //cout << "Hello world!" << endl;
    return 0;
}

明明之前还特意看了一下前缀和 比赛的时候根本没往这里想。。。