题意:有n个士兵 有两个阵营 有m对关系
在每队关系中 有 u v a b c 如果士兵u v 同时属于阵营A 那么军队士气加a 如果同时属于阵营B 那么军队士气加c 其他情况 军队士气加b
显然为两点式求最小割
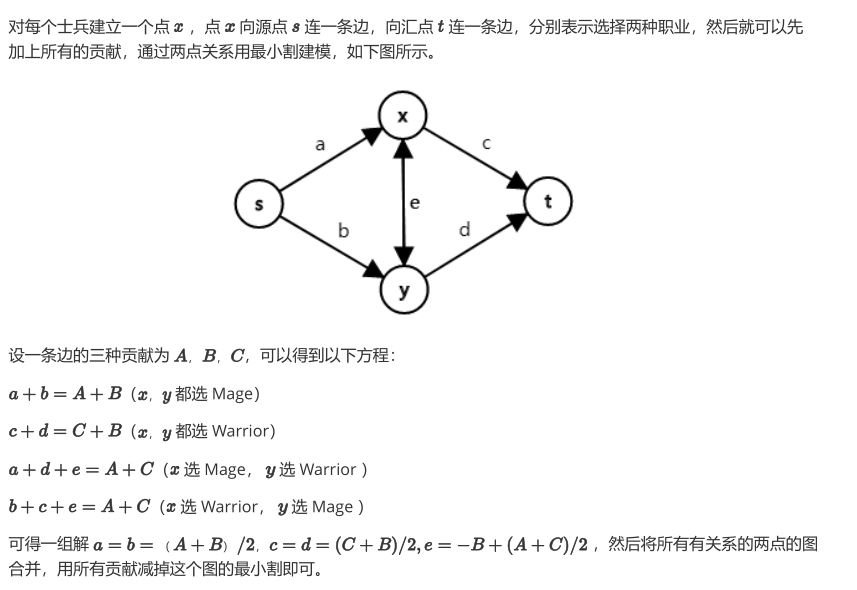
为什么可以/2 进行连 可以尝试进行反证 (找不出反例)
比赛的时候想用如下的连法 但是处理不了两个士兵属于两个阵营的情况
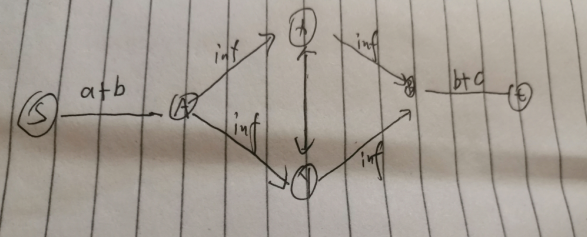

#include<bits/stdc++.h> using namespace std; //input by bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define pb push_back #define REP(i,N) for(int i=0;i<(N);i++) #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// #define inf 0x3f3f3f3f const int N=4e5+44; const int M=4e6+54; struct edge { int to, next; double w; } e[M << 1]; int head[N], cnt = 1; void add(int x, int y, double z) { e[++cnt] = (edge){y, head[x], z}; head[x] = cnt; e[++cnt] = (edge){x, head[y], 0}; head[y] = cnt; } int level[N]; bool bfs(int s, int t) { memset(level, 0, sizeof level); queue<int> q; level[s] = 1; q.push(s); while (!q.empty()) { int pos = q.front(); q.pop(); for (int i = head[pos]; i; i = e[i].next) { int nx = e[i].to; if (!e[i].w || level[nx]) continue; level[nx] = level[pos] + 1; q.push(nx); } } return level[t]; } double dfs(int s, int t, double flow) { if (s == t) return flow; double ret = 0; for (int i = head[s]; flow && i; i = e[i].next) { int nx = e[i].to; if (level[nx] == level[s] + 1 && e[i].w) { double tmp = dfs(nx, t, min(flow, e[i].w)); e[i].w -= tmp; e[i ^ 1].w += tmp; flow -= tmp; ret += tmp; } } if (!ret) level[s] = 0; return ret; } double dinic(int s, int t) { double ret = 0; while (bfs(s, t)) ret += dfs(s, t, inf); return ret; } int n,m,s,t; double a,b,c; int u,v; int main() { while(cin>>n>>m) { cnt=1;CLR(head,0); s=n+10,t=s+1; ll sum=0; while(m--) { scanf("%d%d%lf%lf%lf",&u,&v,&a,&b,&c); add(s,u,(a+b)/2); add(s,v,(a+b)/2); add(u,t,(b+c)/2); add(v,t,(b+c)/2); add(u,v,-b+(a+c)/2); add(v,u,-b+(a+c)/2); sum+=a+b+c; } ll ans=round(sum- dinic(s,t)); cout<<ans<<endl; } return 0; }
