在看一篇论文，其中提到了purity,NMI,ARI，平时只是见到过，具体的含义并不知道，所以就百度整理了下~~
看到了两篇博客，感兴趣的可以看一下~~http://blog.csdn.net/itplus/article/details/10322361 http://blog.csdn.net/sinat_33363493/article/details/52496011
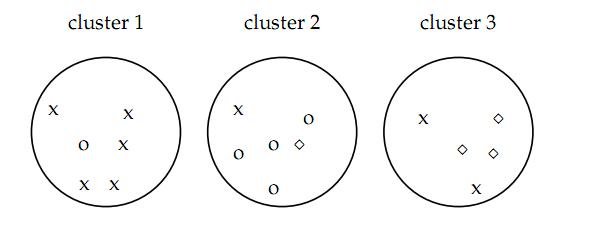
首先看一个例子（PS：别人的~~）认为x代表一类文档，o代表一类文档，方框代表一类文档，聚成了3个cluster，现在要对聚类的结果进行评价
一、purity(纯度)
purity--正确聚类的文档数占总文档的比例 
其中N代表总文档数，Wk代表第k个聚类簇，C = {c1, c2, . . . , cJ}是文档集合，cJ表示第J个文档
例如上面的例子，purity= ( 5+4+3) / 17 = 0.71 第一个cluster正确的有5个，第二个cluster正确的有4个，第3个cluster正确的有3个
这个方法计算简单，值在0~1之间，完全错误值为0，完全正确值为1.
二、Entropy（熵）
对于一个聚类i，首先计算。
指的是聚类 i 中的成员（member）属于类（class）j 的概率，
。其中
是在聚类 i 中所有成员的个数，
是聚类 i 中的成员属于类 j 的个数。
每个聚类的entropy可以表示为，其中L是类（class）的个数。
整个聚类划分的entropy为，其中K是聚类（cluster）的数目，m是整个聚类划分所涉及到的成员个数
例如上面的例子e1=-{1/6log2(1/6)} e2=-{1/6log2(1/6)+1/6log2(1/6)} e3={2/5log2(2/5)} 整个聚类划分的entropy=（6/17)e1+(6/17)e2+(5/17)e3
三、Accuracy(准确率)
比较每一条聚类结果是否和真是的结果一致 
其中N表示文档总数，Ncor表示正确聚类的文档数 准确率和纯度计算一样。
四、NMI（归一化互信息）
互信息指的是两个随机变量之间的关联程度 如下公式计算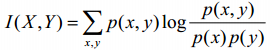
标准互信息是将互信息归一化0~1，通常是除以最大熵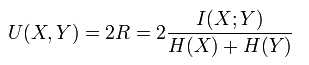
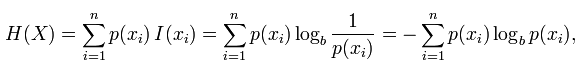
五、ARI（调整兰德指数）
其中C表示实际类别信息，K表示聚类结果，a表示在C与K中都是同类别的元素对数，b表示在C与K中都是不同类别的元素对数
其中表示数据集中可以组成的对数，RI取值范围为[0,1]，值越大意味着聚类结果与真实情况越吻合。
RI越大表示聚类效果准确性越高 同时每个类内的纯度越高
为了实现“在聚类结果随机产生的情况下，指标应该接近零”，调整兰德系数（Adjusted rand index）被提出，它具有更高的区分度：
ARI取值范围为[−1,1]，值越大意味着聚类结果与真实情况越吻合。从广义的角度来讲，ARI衡量的是两个数据分布的吻合程度。
这只是几个指标，聚类结果评价的指标还有很多个。整理论文中提到的几个~~