Real FFT

[文/告别年代   Email：byeyear@hotmail.com]

FFT算法是针对复信号的，而现实场景中很多时候时域是实信号，此时有两种办法加快FFT的速度。

1. 使用一个N点的复FFT同时处理两个N点的实序列

假定我们有两个N点的实序列x[n]和y[n]，它们的FFT具有如下性质：实部偶对称，虚部奇对称。因此可将它们的FFT写为如下形式：

x[n] --F-->  Nyquist以下部分：a+bi；Nyquist以上部分：a-bi

y[n] --F-->  Nyquist以下部分：c+di；Nyquist以上部分：c-di

将这两个实信号拼成一个复信号z=x+yi，因FFT变换满足加法和乘法组合定理，z的FFT变换如下：

z[n] --F-->  Nyquist以下部分：p+qi = a+bi+i(c+di) = (a-d)+(b+c)i，即实部p=a-d, 虚部q=b+c

                 Nyquist以上部分：s+ti = a-bi+i(c-di) = (a+d)+(-b+c)i，即实部s=a+d, 虚部t=-b+c

于是我们可以从z[n]的变换结果p+qi和s+ti分离出x[n]和y[n]的FFT结果：

a=(p+s)/2

b=(q-t)/2

c=(q+t)/2

d=(-p+s)/2

下面是一个稍微正式点的推导：

取z[n]=x[n]+iy[n]

那么：

x[n]=(z[n]+z[n]*)/2

y[n]=-i(z[n]-z[n]*)/2

将上式变换到频域，设x,y,z,z*的FFT系数分别为F_x,F_y,F_z*：

F_x=(F_z+F_z*)/2

F_y=-i(F_z-F_z*)/2

现在来看如何简便地获得F_z*：

F_z*= ∑z[n]^*e^-jk(2π/N)n

   = ∑z[n]^*{e^+jk(2π/N)n}^*

   = {∑z[n]e^+jk(2π/N)n}^*

   = {∑z[n]e^{+jk(2π/N)n-2π}}^*

   = {∑z[n]e^{-j(N-k)(2π/N)n}}^*

因此，F_z*[k]=(F_z[N-k])^*

代入上面的F_x和F_y即可。

2. 使用一个N/2点的复FFT处理一个N点的实序列

 

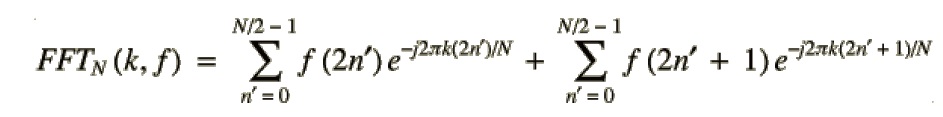
上式中将时域序列拆分为两个序列：偶序列f_e和奇序列f_o，我们可以发现这实际上就是FFT算法推导过程的第一步。

我们已经看过如何用一个N点复FFT计算两个N点实FFT，因此FFT_N/2(k,fe)和FFT_N/2(k,fo)的求解不是问题：

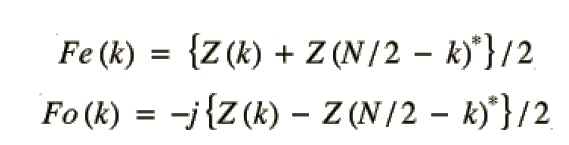
回顾下开头的式子：

上述三个式子组合一下：

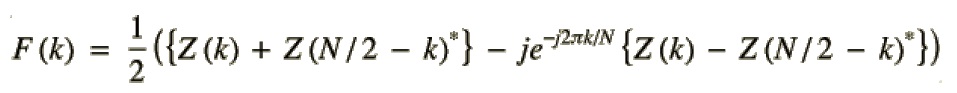
这个就是我们需要的结果。

至此差不多可以完工了，除了F(0)和F(N/2)：这两个值在上式中需要用到Z(N/2)。

根据DFT的周期性，N/2点的复序列FFT满足Z(0)=Z(N/2)，于是F(0)和F(N/2)也有了。

并且对于偶数长度实序列，F(0)和F(N/2)都是实数（实序列FFT满足FFT[k] = FFT^*[n-k]），所以可以把F(N/2)放在F(0)的虚部，这样N点实序列FFT可以用N/2个复数完全表示。

[文/告别年代   Email：byeyear@hotmail.com]