zoukankan html css js c++ java

排序算法

1.快速排序：

快速排序使用分治法（Divide and conquer）策略来把一个序列（list）分为两个子序列（sub-lists）。

步骤为：

从数列中挑出一个元素，称为"基准"（pivot），
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

实现代码：

def lessequal(value1,value2):
    return value1<=value2
def asc(ary,cmp=lessequal):
    if len(ary)<2:
        return ary
    else:
        pivot=ary[0]
        return asc([x for x in ary[1:] if cmp(x,pivot)],cmp)+[pivot]+asc([x for x in ary[1:] if not cmp(x,pivot)],cmp)
def desc(ary,cmp=lessequal):
    if len(ary)<2:
        return ary
    else:
        pivot=ary[0]
        return desc([x for x in ary[1:] if not cmp(x,pivot)],cmp)+[pivot]+desc([x for x in ary[1:] if cmp(x,pivot)],cmp)

分类	排序算法
数据结构	不定
最差时间复杂度	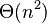$Theta(n^2)$
最优时间复杂度	$Theta(nlog n)$
平均时间复杂度	$Theta(nlog n)$
最差空间复杂度	根据实现的方式不同而不同

2.归并排序：该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

归并操作的过程如下：

申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
设定两个指针，最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
重复步骤3直到某一指针到达序列尾
将另一序列剩下的所有元素直接复制到合并序列尾

实现代码：

def less(value1,value2):
    return value1<value2
def asc(ary,cmp=less):
    if len(ary)<2:
        return ary
    def merge(left,right):
        merged=[]
        while left and right:
            merged.append(left.pop() if not cmp(left[-1],right[-1]) else right.pop())
        while left:
            merged.append(left.pop())
        while right:
            merged.append(right.pop())
        merged.reverse()
        return merged
    middle=int(len(ary)/2)
    left=asc(ary[:middle])
    right=asc(ary[middle:])
    return merge(left,right)
def desc(ary,cmp=less):
    if len(ary)<2:
        return ary
    def merge(left,right):
        merged=[]
        while left and right:
            merged.append(left.pop() if cmp(left[-1],right[-1]) else right.pop())
        while left:
            merged.append(left.pop())
        while right:
            merged.append(right.pop())
        merged.reverse()
        return merged
    middle=int(len(ary)/2)
    left=desc(ary[:middle])
    right=desc(ary[middle:])
    return merge(left,right)

分类	排序算法
数据结构	数组
最差时间复杂度	$Theta(nlog n)$
最优时间复杂度	$Theta(n)$
平均时间复杂度	$Theta(nlog n)$
最差空间复杂度	$Theta(n)$

3.选择排序：在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

实现代码：

def less(value1,value2):
    return value1<value2
def asc(ary,cmp=less):
    n=len(ary)
    for i in range(0,n):
        temp=ary[i]
        index=i
        for j in range(i+1,n,1):
            if cmp(ary[j],temp):
                index=j
                temp=ary[j]
        ary[i],ary[index]=ary[index],ary[i]
    return ary
def desc(ary,cmp=less):
    n=len(ary)
    for i in range(0,n):
        temp=ary[i]
        index=i
        for j in range(i+1,n,1):
            if not cmp(ary[j],temp):
                index=j
                temp=ary[j]
        ary[i],ary[index]=ary[index],ary[i]
    return ary

分类	排序算法
数据结构	数组
最差时间复杂度	О(n²)
最优时间复杂度	О(n²)
平均时间复杂度	О(n²)
最差空间复杂度	О(n) total, O(1)auxiliary

4.插入排序：通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

实现代码：

def less(value1,value2):
    return value1<value2
def asc(ary,cmp=less):
    n=len(ary)
    for i in range(1,n):
        if cmp(ary[i],ary[i-1]):
            temp=ary[i]
            index=i
            for j in range(i-1,-1,-1):
                if not cmp(ary[j],temp):
                    ary[j+1]=ary[j]
                    index=j
                else:
                    break
            ary[index]=temp
    return ary
def desc(ary,cmp=less):
    n=len(ary)
    for i in range(1,n):
        if not cmp(ary[i],ary[i-1]):
            temp=ary[i]
            index=i
            for j in range(i-1,-1,-1):
                if cmp(ary[j],temp):
                    ary[j+1]=ary[j]
                    index=j
                else:
                    break
            ary[index]=temp
    return ary

分类	排序算法
数据结构	数组
最差时间复杂度	$O(n^2)$
最优时间复杂度	$O(n)$
平均时间复杂度	$O(n^2)$
最差空间复杂度	总共 $O(n)$ ，需要辅助空间 $O(1)$

5.希尔排序：

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

例如，假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]，如果我们以步长为5开始进行排序，我们可以通过将这列表放在有5列的表中来更好地描述算法，这样他们就应该看起来是这样：

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后我们对每列进行排序：

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

将上述四行数字，依序接在一起时我们得到：[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了，然后再以3为步长进行排序：

排序之后变为：

最后以1步长进行排序（此时就是简单的插入排序了）。

代码实现：

def less(value1,value2):
    return value1<value2
def asc(ary,cmp=less):
    n=len(ary)
    gap=int(round(n/2))#初始步长，用round四舍五入取整
    while gap>0:
        for i in range(gap,n):#每一列进行插入排序，从gap到n-1
            if not cmp(ary[i-gap],ary[i]):
                temp=ary[i]
                index=i
                for j in range(i-gap,-1,-gap):#插入排序
                    if not cmp(ary[j],temp):
                        ary[j+gap]=ary[j]
                        index=j
                    else:
                        break
                ary[index]=temp
        gap=int(round(gap/2))#重新设置步长
    return ary
def desc(ary,cmp=less):
    n=len(ary)
    gap=int(round(n/2))#初始步长，用round四舍五入取整
    while gap>0:
        for i in range(gap,n):#每一列进行插入排序，从gap到n-1
            if cmp(ary[i-gap],ary[i]):
                temp=ary[i]
                index=i
                for j in range(i-gap,-1,-gap):#插入排序
                    if cmp(ary[j],temp):
                        ary[j+gap]=ary[j]
                        index=j
                    else:
                        break
                ary[index]=temp
        gap=int(round(gap/2))#重新设置步长
    return ary

分类	排序算法
数据结构	数组
最差时间复杂度	根据步长序列的不同而不同。已知最好的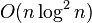： $O(nlog^2 n)$
最优时间复杂度	O(n)
平均时间复杂度	根据步长序列的不同而不同。
最差空间复杂度	O(n)

6.冒泡排序：比较相邻的的两个元素，并将大(小的)往后(前)移动。

实现代码：

def asc(ary):
    n=len(ary)
    for i in range(n):
        for j in range(0,n-i-1):
            if not less(ary[j],ary[j+1]):
                ary[j],ary[j+1]=ary[j+1],ary[j]
    return ary
def desc(ary):
    n=len(ary)
    for i in range(0,n):
        for j in range(n-2,i-1,-1):
            if less(ary[j],ary[j+1]):
                ary[j],ary[j+1]=ary[j+1],ary[j]
    return ary
def less(value1,value2):
    return value1<value2

分类	排序算法
数据结构	数组
最差时间复杂度	$O(n^2)$
最优时间复杂度	$O(n)$
平均时间复杂度	$O(n^2)$
最差空间复杂度	总共 $O(n)$ ，需要辅助空间 $O(1)$

6.堆排序

堆排序在 top K 问题中使用比较频繁。堆排序是采用二叉堆的数据结构来实现的。该结构虽然实质上还是一维数组但近似完全二叉树并同时满足堆积性质：父节点的值大于（小于）子节点的值。

访问相关节点：

对于大小为n的一维数组，数组中的下标为1~n-1

父节点i的左子节点在位置(2*i+1);
父节点i的右子节点在位置(2*i+2);
子节点i的父节点在位置floor((i-1)/2);

堆中定义以下几种操作：

最大堆调整（Max_Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
创建最大堆（Build_Max_Heap）：将堆所有数据重新排序
堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整运算

实现代码：

 1 def heap_sortasc(ary):
 2     n=len(ary)
 3     first=int(n/2)-1#z最后一个非叶子节点
 4     for start in range(first,-1,-1):#构造大根堆
 5         max_heapify(ary,start,n)
 6     for end in range(n-1,-1,-1):#堆排，将大根堆转换成有序数组
 7         ary[end],ary[0]=ary[0],ary[end]
 8         max_heapify(ary,0,end)
 9     return ary
10 #最大堆调整，将堆的末端子节点作调整，使得子节点永远小于父节点
11 #start为当前需要调整
12 #递归实现
13 def  max_heapify(ary,root,size):
14     while True:
15         child=root*2+1#调整节点的子节点
16         if root<int(size/2):
17             if child+1<size and less(ary[child],ary[child+1]):
18                 child=child+1#取较大的子节点
19             if less(ary[root],ary[child]):#较大的子节点成为父节点
20                 ary[root],ary[child]=ary[child],ary[root]#变换
21                 root=child
22             else:
23                 break
24         else:
25             break
26 def heap_sortdesc(ary):
27     n=len(ary)
28     first=int(n/2)-1#z最后一个非叶子节点
29     for start in range(first,-1,-1):#构造小根堆
30         min_heapify(ary,start,n)
31     for end in range(n-1,-1,-1):#堆排，将小根堆转换成有序数组
32         ary[end],ary[0]=ary[0],ary[end]
33         min_heapify(ary,0,end)
34     return ary
35 #最小堆调整，将堆的末端子节点作调整，使得子节点永远大于父节点
36 #start为当前需要调整
37 #递归实现
38 def  min_heapify(ary,root,size):
39     while True:
40         child=root*2+1#调整节点的子节点
41         if root<int(size/2):
42             if child+1<size and less(ary[child],ary[child+1])==False:
43                 child=child+1#取较小的子节点
44             if less(ary[root],ary[child])==False:#较小的子节点成为父节点
45                 ary[root],ary[child]=ary[child],ary[root]#变换
46                 root=child
47             else:
48                 break
49         else:
50             break
51 def less(value1,value2):
52     return value1<value2

算法复杂度：

分类
数据结构	数组
最差时间复杂度	$O(n log n)$
最优时间复杂度	$O(n log n)$
平均时间复杂度	$Theta(n log n)$
最差空间复杂度	$O(n)$ total, $O(1)$ auxiliary

reference:

1.http://zh.wikipedia.org/wiki/快速排序

1.http://zh.wikipedia.org/wiki/归并排序

2.http://zh.wikipedia.org/wiki/选择排序

3.http://zh.wikipedia.org/wiki/插入排序

4.http://zh.wikipedia.org/wiki/希尔排序

5.http://zh.wikipedia.org/wiki/冒泡排序

6.http://zh.wikipedia.org/wiki/堆排序

查看全文

相关阅读:
Linux Exploit系列之一典型的基于堆栈的缓冲区溢出
 [Codeforces Round #433][Codeforces 853C/854E. Boredom]
Educational Codeforces Round 4
[Educational Round 3][Codeforces 609F. Frogs and mosquitoes]
[ACM-ICPC 2018 徐州赛区网络预赛][D. Easy Math]
Educational Codeforces Round 50
[Codeforces Round #507][Codeforces 1039C/1040E. Network Safety]
[Educational Round 3][Codeforces 609E. Minimum spanning tree for each edge]
Educational Codeforces Round 3
[Manthan, Codefest 18][Codeforces 1037E. Trips]

原文地址：https://www.cnblogs.com/bzsh/p/4474301.html