题面
题解
我似乎连积分都不太熟练→_→
总之就是对于一个原函数,我们找一个二次函数来近似它,那么有
[egin{aligned}
int_a^bf(x)dx
&approxint_a^bAx^2+Bx+C\
&=frac{A}{3}(b^3-a^3)+frac{B}{2}(b^2-a^2)+C(a-b)\
&=frac{(b-a)}{6}(2A(b^2+ab+a^2)+3B(b+a)+6C)\
&=frac{(b-a)}{6}(2Ab^2+2Aab+2Aa^2+3Bb+3Ba+6C)\
&=frac{(b-a)}{6}(Aa^2+Ba+C+Ab^2+Bb+C+4A(frac{a+b}{2})^2+4B(frac{a+b}{2})+4C)\
&=frac{(b-a)}{6}(f(a)+f(b)+4f(frac{a+b}{2}))\
end{aligned}
]
然后自适应(Simpson)就是用来调整精度的,具体可以看代码
ps:关于代码里那个诡异的(leq 15 cdot eps),据说是因为这么一个结论: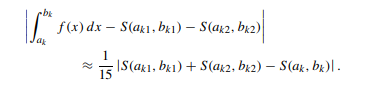
//minamoto
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
using namespace std;
double a,b,c,d,l,r;
inline double f(const R double &x){return (c*x+d)/(a*x+b);}
inline double simpson(const R double l,const R double r){
R double mid=(l+r)/2;
return (f(l)+4*f(mid)+f(r))*(r-l)/6;
}
double ask(double l,double r,double eps,double ans){
double mid=(l+r)/2,ql=simpson(l,mid),qr=simpson(mid,r);
if(fabs(ql+qr-ans)<=15*eps)return ql+qr+(ql+qr-ans)/15;
return ask(l,mid,eps/2,ql)+ask(mid,r,eps/2,qr);
}
int main(){
// freopen("testdata.in","r",stdin);
scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&l,&r);
printf("%.6lf
",ask(l,r,1e-6,simpson(l,r)));
return 0;
}