斜率优化真是大坑……太考验思维了……然而似乎只要懂了之后所有题都能做了……就看你能不能把状态转移方程给抠出来……
借鉴的文章比较多……就不一一列举了……主要是莫名其妙看了两种方法的说明然后完全懵逼不知道谁对谁错,后来才发现两种是从不同的角度去说明的
首先我们要知道,对于形如$dp[i]=a[j]+b[j]$的式子,可以用单调队列优化到$O(n)$
但如果式子变成了形如$dp[i]=a[i]*b[j]+c[i]+d[j]$的时候,因为$a[i]*b[j]$这一项既与$i$有关又与$j$有关,所以直接单调队列行不通了
我们先来考虑这一道题目,设前缀和为$sum[i]$转移方程应该是$$dp[i]=min(dp[j]+(sum[i]+i-sum[j]-j-L-1)^2) (j<i)$$
那么我们要考虑一下进行优化,我们假设选取$j$会比$k$更优,且$k<j$
那么$$dp[j]+(sum[i]+i-sum[j]-j-L-1)^2<dp[k]+(sum[i]+i-sum[k]-k-L-1)^2$$
然后为了方便一点,令$a[i]=sum[i]+i,b[i]=sum[i]+i+L+1$
那么上式可以化为$$dp[j]+(a[i]-b[j])^2<dp[k]+(a[i]-b[k])^2$$
然后展开一下$$dp[j]+a[i]^2-2*a[i]*b[j]+b[j]^2<dp[k]+a[i]^2-2*a[i]*b[k]+b[k]^2$$
移项$$dp[j]+b[j]^2-dp[k]-b[k]^2<2*a[i]*b[j]-2*a[i]*b[k]$$
$$frac {dp[j]+b[j]^2-dp[k]-b[k]^2}{b[j]-b[k]}<2*a[i]$$
然后令$Y[i]=dp[i]+b[i]^2,x[i]=b[i]$
那么原式可化为$$frac {Y[j]-Y[k]}{X[j]-X[k]}<2*a[i]$$
所以如果$j>k$且$frac {Y[j]-Y[k]}{X[j]-X[k]}<2*a[i]$ 那么$j$比$k$更优,否则$k$比$j$优
所以证了半天这有啥用么?没有
我们考虑一下,若在平面直角坐标系上存在点$k:(X[k],Y[k])$与$j:(X[j],Y[j])$,那么$frac {Y[j]-Y[k]}{X[j]-X[k]}$就是两点的斜率
然后一下我们用$slope(i,j)$表示$i,j$两点的斜率,即$frac {Y[i]-Y[j]}{X[i]-X[j]}$
因为$X[j],X[k],Y[i],Y[k]$都是定值,所以上面两个点都是定点
然后我们假设有三个值$i,j,k$(这里的$i$与上面的无关),其中$k<j<i$
我们假设$slope(j,k)>slope(i,j)$,也就是说是下面这个样子
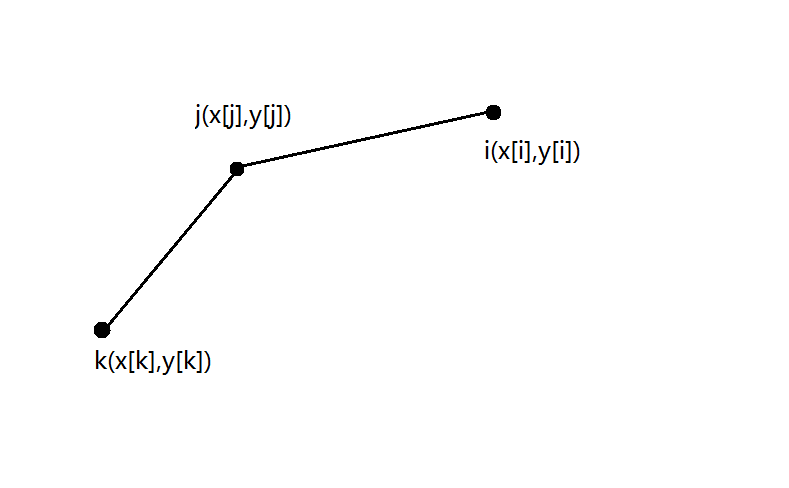
那么$slope(j,k),slope(i,j),2*a[i]$会有三种大小关系
当$slope(j,k)>slope(i,j)>2*a[i]$时,$j$比$i$优,$k$比$j$优,$j$不是最优
当$slope(j,k)>2*a[i]>slope(i,j)$时,$k$比$j$优,$i$比$j$优,$j$不是最优
当$2*a[i]>slope(j,k)>slope(i,j)$时,$j$比$k$优,$i$比$j$优,$j$不是最优
也就是说,如果存在$slope(j,k)>slope(i,j)$,那么从$j$转移无论如何都不可能是最优的方案,已经可以把它给排除了
所以,我们必须保证维护的是一个下凸包,即$slope(j,k)>slope(i,j)$,如下图
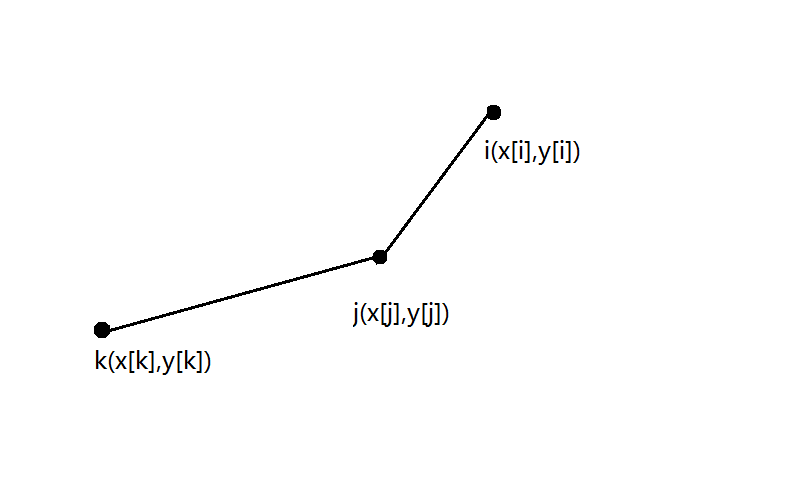
不难看出下凸包的斜率是永远单调递增的,那么可以用一个单调队列来维护,即每一次看一看最末尾的元素$slope(q[t],q[t-1])<slope(q[t],i)$是否成立,若不成立则把$q[t]$弹出(即$--t$)
或者写成$slope(q[t],q[t-1])<slope(q[t-1],i)$也是可以的(仔细观察上图,不难发现这两个判断是等价的)
那么,在这个单调队列里哪一个答案才是最优的呢?
因为只有$slope(j,k)<2*a[i]$时$j$才会比$k$更优,而因为$a[i]=sum[i]+i$(忘了的可以回去看看,上面的假设),所以$s[i]$肯定是递增的
那么如果$slope(j,k)>2*a[i]$,那么$j$就不可能比$k$更优了,否则$j$一定比$k$优,所以我们可以把$k$从单调队列里删掉了,即每一次看看最开头的元素$slope(q[h],q[h+1])<2*a[i]$是否成立,若成立,则把$q[h]$弹出(即$++h$)
那么每一次单调队列的开头都满足$slope(q[h],q[h+1])>2*a[i]$,即$q[h]$后面的答案永远不可能比它更优。所以我们可以直接用$q[h]$来进行转移就行了,时间复杂度为$O(n)$
顺便注意一个细节,因为我们要求的$j$必须小于$i$所以我们应该先处理完单调队列开头并更新完答案,再去处理末尾
然后上本题代码
1 //minamoto 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #define db double 6 #define ll long long 7 using namespace std; 8 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 9 char buf[1<<21],*p1=buf,*p2=buf; 10 inline int read(){ 11 #define num ch-'0' 12 char ch;bool flag=0;int res; 13 while(!isdigit(ch=getc())) 14 (ch=='-')&&(flag=true); 15 for(res=num;isdigit(ch=getc());res=res*10+num); 16 (flag)&&(res=-res); 17 #undef num 18 return res; 19 } 20 const int N=50005; 21 int n,L; 22 db sum[N],dp[N];int h,t,q[N]; 23 inline db a(int i){return sum[i]+i;} 24 inline db b(int i){return sum[i]+i+L+1;} 25 inline db X(int i){return b(i);} 26 inline db Y(int i){return dp[i]+b(i)*b(i);} 27 inline db slope(int i,int j){return (Y(i)-Y(j))/(X(i)-X(j));} 28 //这些都如上面定义,忘了的再去看看 29 int main(){ 30 n=read(),L=read(); 31 for(int i=1;i<=n;++i) sum[i]=read()+sum[i-1]; 32 h=t=1; 33 //一开始要先放一个0,而不能把它设为空 34 for(int i=1;i<=n;++i){ 35 while(h<t&&slope(q[h],q[h+1])<2*a(i)) ++h; 36 double p=a(i)-b(q[h]); 37 dp[i]=dp[q[h]]+p*p; 38 //更新答案 39 while(h<t&&slope(q[t-1],q[t])>slope(q[t-1],i)) --t; 40 q[++t]=i; 41 } 42 printf("%lld ",(ll)dp[n]); 43 return 0; 44 }