Gosha is hunting 题解，带权二分模板

由于刚学带权二分，所以考虑带权二分
对于dp优化型题目，首先写出普通dp方程，(f_{i,a,b})表示前i个宝可梦用a个精灵球和b个超级球期望能抓住几只

[f_{i,a,b}=max(f_{i-1,a-1,b}+p_{i},f_{i-1,a,b-1}+q_{i},f_{i-1,a-1,b-1}+q_{i} * p_{i}-q_{i}*p_{i}) ]

我们发现一只宝可梦用一只球会比两只球有性价比(毕竟还要减(p[i]*q[i]) (注意两只球若都抓住只贡献一次)）)

所以当(i,a)固定时，关于(b)的函数(f_{i,a,b})是上凸的，于是我们脑中就有了一个最优解图像：

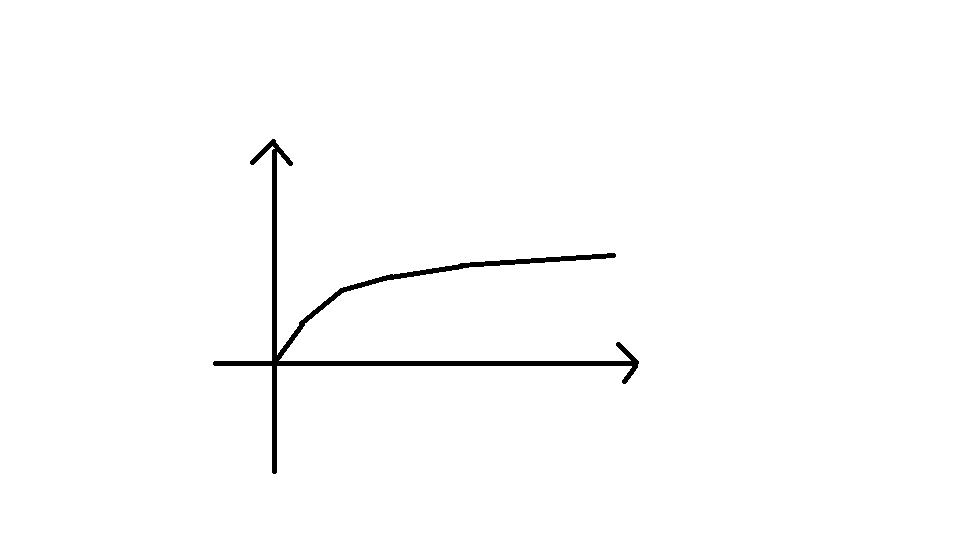
然而这只是脑中的，我们要想办法根据他的性质把他还原出来
这里就有一个针对凸函数的办法：引一条直线使该直线与函数相切，这个函数也是由一小节一小节线段构成的(毕竟大家都是整数)，当相切时实际上引的直线就是那一条线段比如：

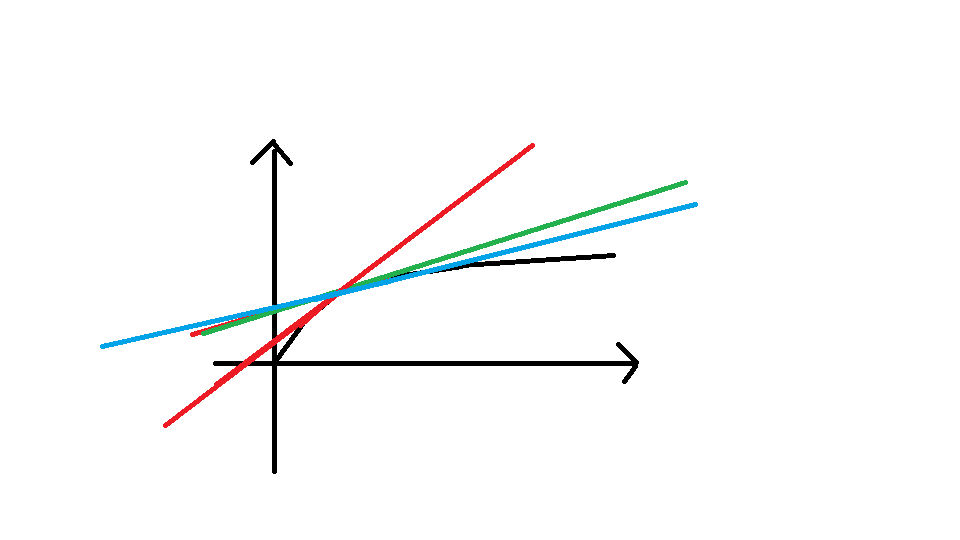
而我们想要得到的是在正确函数上当(x=b)时的取值，所以我们不断调整斜率，因为该函数是凸函数，当截距最大时，我们得到的就是最优函数图像最右端的部分，我们口胡设一个函数

[f'(x)=f(x)+kx ]

这就是我们拿来还原图像的直线((f'(x))为最优(f_{n,a,x}))，变形一下

[f(x)=f'(x)-kx ]

这下我们表示出了截距，我们要想办法让截距最大
发现(kx)很像一个权值，所以我们让超级球的收益变为(q[i]-k)，然后贪心做就好，细节可以看代码(作死用了提前声明请见谅)

(update)

看到了01分数规划，知道了一个结论
若(f(n)<0) 当前mid大于真答案
若(f(n)>0) 当前mid小于真答案
放在带权二分同样适用

#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
#define ld double
#define mid ((l+r)/2)
using namespace std;
ll n,a,b;
ld p[10001],q[10001],f[2010][2010],cnt[2101][2101];

bool check_dp(ld sam);

int main(){
	scanf("%lld%lld%lld",&n,&a,&b);
	for(ll i=1;i<=n;i++)scanf("%lf",&p[i]);
	for(ll i=1;i<=n;i++)scanf("%lf",&q[i]);
	ld l=0,r=1,ans=1;
	for(ll o=1;o<=60;o++){
		if(check_dp(mid))ans=mid,r=mid-1;
		else l=mid+1;
	}
	ans=f[n][a]+ans*b;
	printf("%.5lf
",ans);
}

bool check_dp(ld sam){
	memset(f,0,sizeof f);
	memset(cnt,0,sizeof cnt);
	ll i,j;
	for(i=1;i<=n;i++){
		for(j=0;j<=a;j++){
			cnt[i][j]=cnt[i-1][j];
			f[i][j]=f[i-1][j];
			if(j!=0&&f[i-1][j-1]+p[i]>f[i][j]){
				cnt[i][j]=cnt[i-1][j-1];
				f[i][j]=p[i]+f[i-1][j-1];
			}
			if(f[i-1][j]+q[i]-sam>f[i][j]){
				cnt[i][j]=cnt[i-1][j]+1;
				f[i][j]=f[i-1][j]+q[i]-sam;
			}
			if(j!=0&&f[i-1][j-1]+p[i]+q[i]-q[i]*p[i]-sam>f[i][j]){
				cnt[i][j]=cnt[i-1][j-1]+1;
				f[i][j]=f[i-1][j-1]+p[i]+q[i]-q[i]*p[i]-sam;
			}
		}
	}
	return cnt[n][a]<=b;
}