js内置的Array函数原型对象有个sort方法,这个方法能按照顺序排序数组。
例如:
1 var arr1 = [6, 4, 2, 5, 2]; 2 arr1.sort((x, y) => x - y); 3 console.log(arr1); // [2, 2, 4, 5, 6];
以升序为例,这个方法的实现原理的简单理解:
第一轮比较。
先拿第一个数和第二个数字比较,如果第一个比第二个大,则交换位置。
接着又拿第一个数和第三个数比较,如果第一个比第三个大,则交换位置。
。。。
最后拿第一个数与最后一个数比较,如果第一个数比最后一个数大,则交换位置。
以上是第一轮比较。经过第一轮的比较。第一个数,就是数组中值最小的数了。
用上述例子来描述第一轮比较的过程,如图:
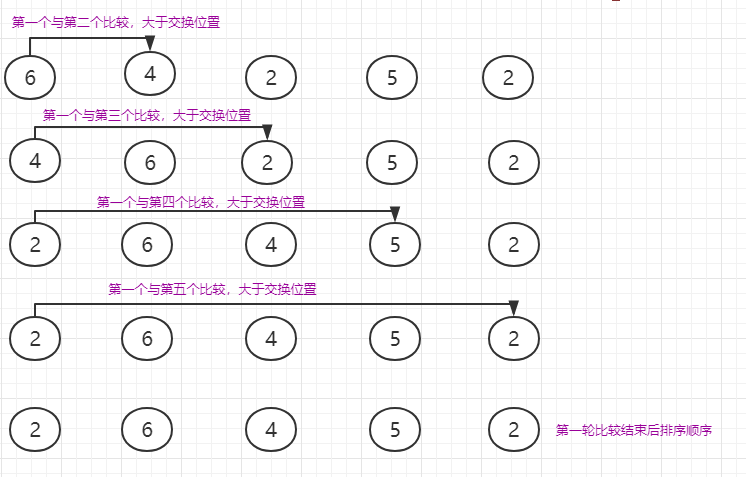
接着开始第二轮比较
先拿第二个数与第三个数比较,如果第二个比第三个大,则交换位置。
然后又拿第二个数和第四个数比较,如果第二个比第四个大,则交换位置。
。。。
最后拿第二个数与最后一个数比较,如果第二个数比最后一个数大,则交换位置。
以上是第二轮比较。经过第二轮的比较。第二个数,就是数组中值的第二小的数了。
用上述例子来描述第二轮比较的过程,如图:
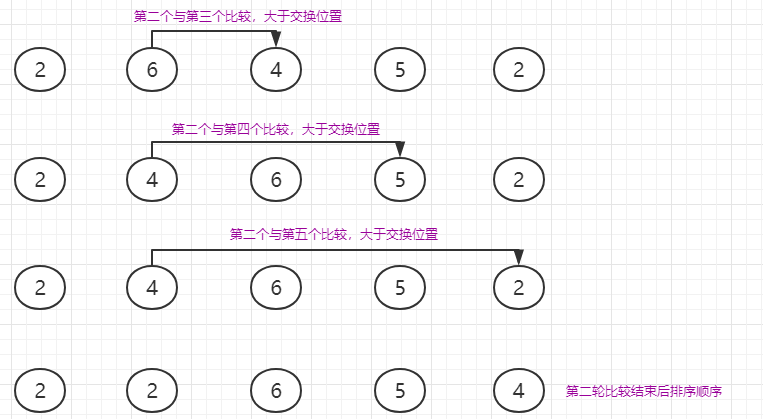
循环往复直至全部都比较完。
上述例子的比较过程的代码演示:
1 function mySort(arr, cb) { 2 window.count = 0;// 统计循环次数 3 const res = cb && cb(1, 2); 4 let i, j, len = arr.length; 5 if (res < 0) {// 升序 6 for (i = 0; i < len; i++) { 7 for (j = i + 1; j < len; j++) { 8 count++; 9 if (arr[i] > arr[j]) { 10 [arr[i], arr[j]] = [arr[j], arr[i]]; 11 } 12 } 13 } 14 } else {// 降序 15 for (i = 0; i < len; i++) { 16 for (j = i + 1; j < len; j++) { 17 count++; 18 if (arr[i] < arr[j]) { 19 [arr[i], arr[j]] = [arr[j], arr[i]]; 20 } 21 } 22 } 23 } 24 }
这种排序方法循环次数为 (len - 1) * len / 2。
验证:
1 const arr = []; 2 for (let i = 0; i < 10; i++) { 3 arr.push(Math.floor(Math.random()*100)); 4 } 5 mySort(arr, (x, y) => x - y);
结果:
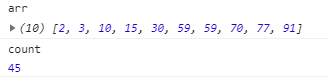
采用排序二叉树结构的算法。代码演示:
1 function mySort(arr, cb) { 2 const res = cb && cb(1 ,2); 3 class Node { 4 constructor(key) { 5 this.key = key; 6 this.left = null; 7 this.right = null; 8 } 9 }; 10 class BinaryTree { 11 constructor(key) { 12 this.root = null; 13 this.init(key); 14 } 15 init(key) { 16 this.root = new Node(key); 17 } 18 insert(key) { 19 const newNode = new Node(key); 20 this._insertNode(this.root, newNode); 21 } 22 _insertNode(root, node) { 23 if (node.key < root.key) { 24 if (!root.left) { 25 root.left = node; 26 } else { 27 this._insertNode(root.left, node); 28 } 29 } else { 30 if (!root.right) { 31 root.right = node; 32 } else { 33 this._insertNode(root.right, node); 34 } 35 } 36 } 37 inorderTraversal(callback) { 38 if (res < 0) { 39 this._inorderTraversalNodeSmall(this.root, callback); 40 } else { 41 this._inorderTraversalNodeBig(this.root, callback); 42 } 43 } 44 _inorderTraversalNodeSmall(node, callback) { 45 if (!!node) { 46 this._inorderTraversalNodeSmall(node.left, callback); 47 callback(node); 48 this._inorderTraversalNodeSmall(node.right, callback); 49 } 50 } 51 _inorderTraversalNodeBig(node, callback) { 52 if (!!node) { 53 this._inorderTraversalNodeBig(node.right, callback); 54 callback(node); 55 this._inorderTraversalNodeBig(node.left, callback); 56 } 57 } 58 } 59 60 const binaryTree = new BinaryTree(arr[0]); 61 let i, len; 62 for(i = 1, len = arr.length; i < len; i++) { 63 binaryTree.insert(arr[i]); 64 } 65 const _arr = []; 66 binaryTree.inorderTraversal(node => { 67 _arr.push(node.key); 68 }); 69 return _arr; 70 }
测试:
1 const arr = []; 2 for (let i = 0; i < 10; i++) { 3 arr.push(Math.floor(Math.random()*100)); 4 } 5 const newArr1 = mySort(arr, (x, y) => y - x); 6 const newArr2 = mySort(arr, (x, y) => x - y);
结果:

当数组比较大的时候,后面这种算法的优势明显。
现以后面这种算法为例,测试代码:
1 const arr = []; 2 for (let i = 0; i < 5000000; i++) { 3 arr.push(Math.floor(Math.random()*50000000)); 4 } 5 const time = new Date().getMinutes() + ':' + new Date().getSeconds(); 6 mySort(arr, (x, y) => x - y); 7 const nextTime = new Date().getMinutes() + ':' + new Date().getSeconds();
结果:

数组长度为5000000时,函数大概运行了6秒。
如果以第一种算法为例,5000000估计要好几分钟,这里缩减一下,设置成50000。测试代码:
1 const arr = []; 2 for (let i = 0; i < 50000; i++) { 3 arr.push(Math.floor(Math.random()*50000000)); 4 } 5 const time = new Date().getMinutes() + ':' + new Date().getSeconds(); 6 mySort(arr, (x, y) => x - y); 7 const nextTime = new Date().getMinutes() + ':' + new Date().getSeconds();
结果:
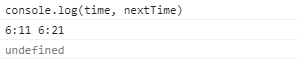
数组长度为50000时,函数大概运行了10秒。
第一种算法的耗时貌似也不是平滑增加的。估计也是一条陡峭的曲线。数学知识都忘光了。以后搞明白了在来完善。