matlab学习——05插值和拟合(一维二维插值,拟合)

05插值和拟合

1.一维插值

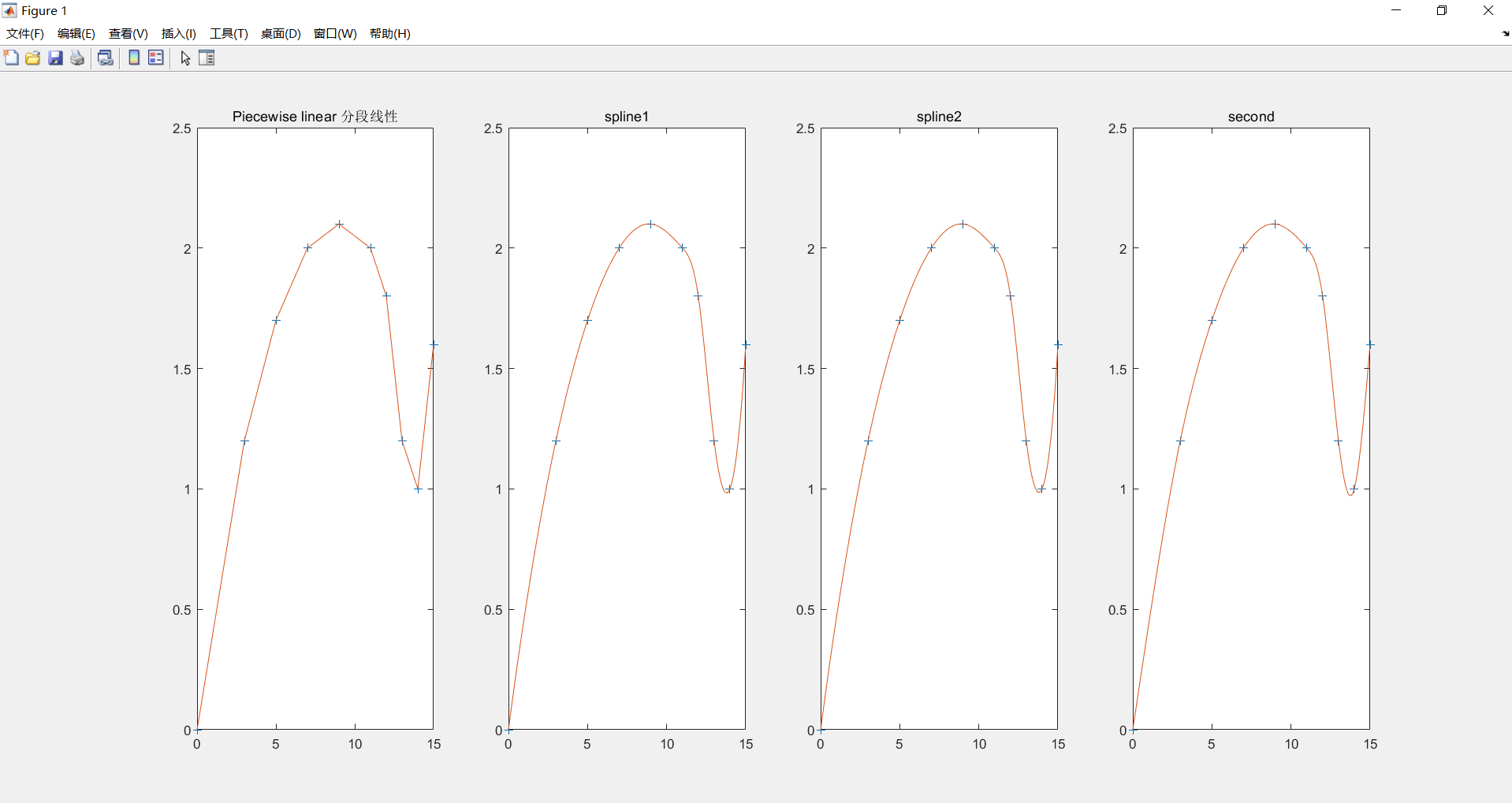
(1) 机床加工零件，试用分段线性和三次样条两种插值方法计算。并求x=0处的曲线斜率和13<=x<=15范围内y的最小值。

x0=[0 3 5 7 9 11 12 13 14 15];
y0=[0 1.2 1.7 2 2.1 2.0 1.8 1.2 1.0 1.6];
x=0:0.1:15;
% interp1现有插值函数，要求x0单调，'method'有
% nearest 最近项插值   linear 线性插值
% spline 立方样条插值  cubic 立方插值
y1=interp1(x0,y0,x); 

y2=interp1(x0,y0,x,'spline');

pp1=csape(x0,y0);
y3=fnval(pp1,x);

pp2=csape(x0,y0,'second');
y4=fnval(pp2,x);

[x',y1',y2',y3',y4']

subplot(1,4,1)
plot(x0,y0,'+',x,y1)
title('Piecewise linear 分段线性')

subplot(1,4,2)
plot(x0,y0,'+',x,y2)
title('spline1')

subplot(1,4,3)
plot(x0,y0,'+',x,y3)
title('spline2')

subplot(1,4,4)
plot(x0,y0,'+',x,y4)
title('second')

dx=diff(x);
dy=diff(y3);
dy_dx=dy./dx;
dy_dx0=dy_dx(1);
ytemp=y3(131:151);
ymin=min(ytemp);
index=find(y3==ymin);
xmin=x(index);
[xmin,ymin]

(2)  已知速度的四个观测值,用三次样条求位移S=0.15到0.18上的vd(t)积分

t   0.15    0.16     0.17    0.18
vt   3.5    1.5       2.5       2.8

format compact;
% 已知速度的四个观测值,用三次样条求位移S=0.15到0.18上的vd(t)积分
% t   0.15  0.16  0.17  0.18
% vt  3.5   1.5    2.5   2.8
clc,clear
x0=0.15:0.01:0.18;
y0=[3.5 1.5 2.5 2.8];
% csape 三次样条插值,返回要求插值的的函数值
pp=csape(x0,y0) % 默认的边界条件,Lagrange边界条件
format long g
xishu = pp.coefs % 显示每个区间上三次多项式的系数
s=quadl(@(t)ppval(pp,t),0.15,0.18) % 求积分
format % 恢复短小数的显示格式

% 画图
t=0.15:0.001:0.18;
y=fnval(pp,t);
plot(x0,y0,'+',t,y)

pp = 
  包含以下字段的 struct:

      form: 'pp'
    breaks: [0.1500 0.1600 0.1700 0.1800]
     coefs: [3×4 double]
    pieces: 3
     order: 4
       dim: 1
xishu =
  1 至 2 列
         -616666.666666667                     33500
         -616666.666666667                     15000
         -616666.666666668         -3499.99999999999
  3 至 4 列
         -473.333333333334                       3.5
          11.6666666666671                       1.5
          126.666666666667                       2.5
s =
                  0.068625

2.二维插值

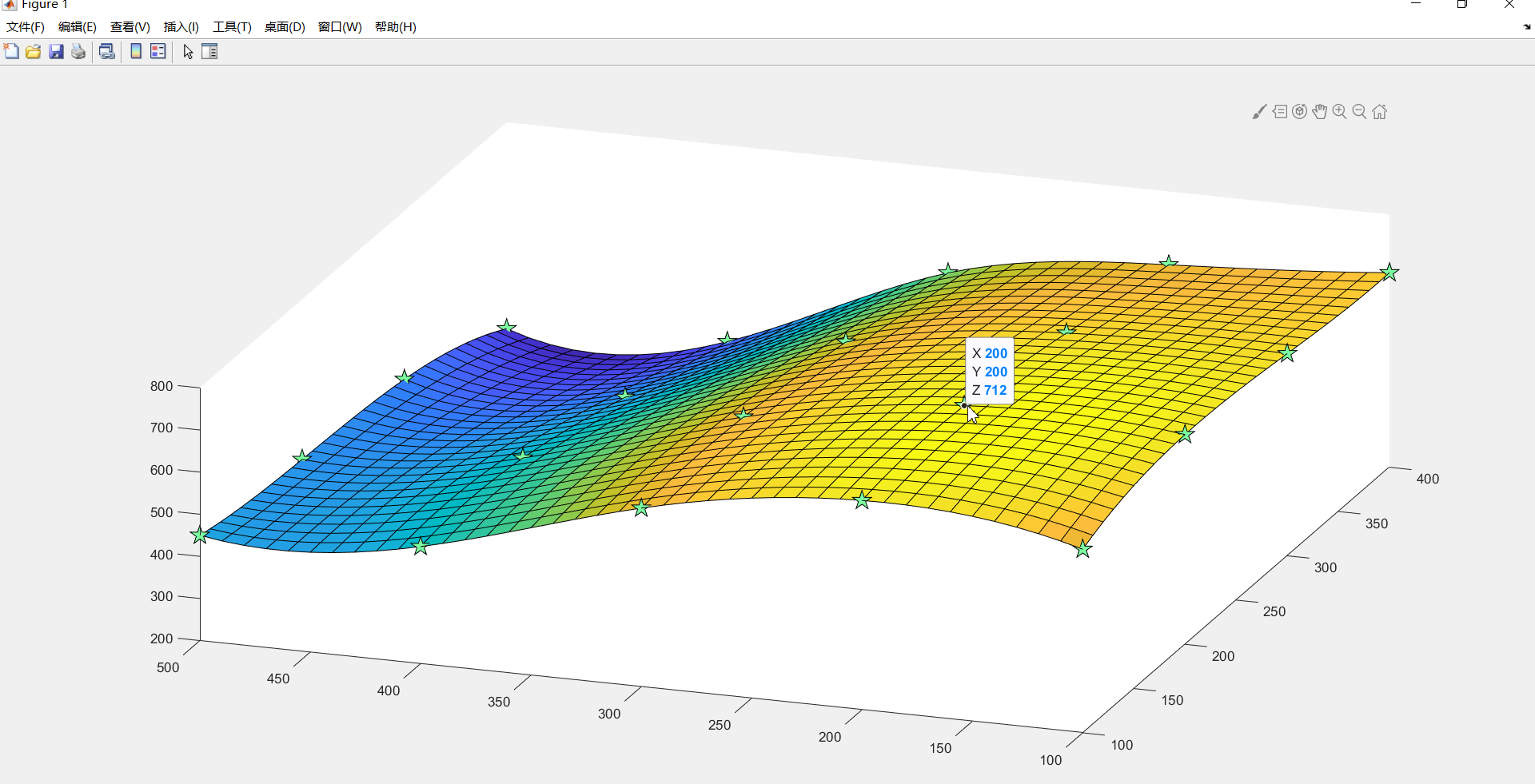
(1) 丘陵测量高度。试插值一曲面，确定合适的模型，并由此找出最高的和该点的最高程。

format compact;
% 丘陵,在x,y方向上每隔100m测个点
clear,clc
x=100:100:500;
y=100:100:400;
z=[636 697 624 478 450
    698 712 630 478 420
    680 674 598 412 400
    662 626 552 334 310];

pp=csape({x,y},z') % 三次样条,返回函数
xi=100:10:500;
yi=100:10:400;
cz=fnval(pp,{xi,yi}); % 得到插值后的z

[i,j]=find(cz==max(max(cz))) % 找最高点的地址
xm=xi(i),ym=yi(i),zmax=cz(i,j) % 求最高点的坐标

% 画图
[X,Y]=meshgrid(yi,xi);%构造1×1网格，20×20个
[X0,Y0]=meshgrid(y,x);%构造1×1网格，20×20个 
plot3(X0,Y0,z,'p', 'MarkerEdgeColor','k','MarkerSize',15 ,'MarkerFaceColor',[.49 1 .63])
hold on
% mesh(X,Y,cz)
surf(X,Y,cz)

pp = 
  包含以下字段的 struct:

      form: 'pp'
    breaks: {[100 200 300 400 500]  [100 200 300 400]}
     coefs: [1×16×12 double]
    pieces: [4 3]
     order: [4 4]
       dim: 1
i =
     8
j =
     9
xm =
   170
ym =
   170
zmax =
  720.6252

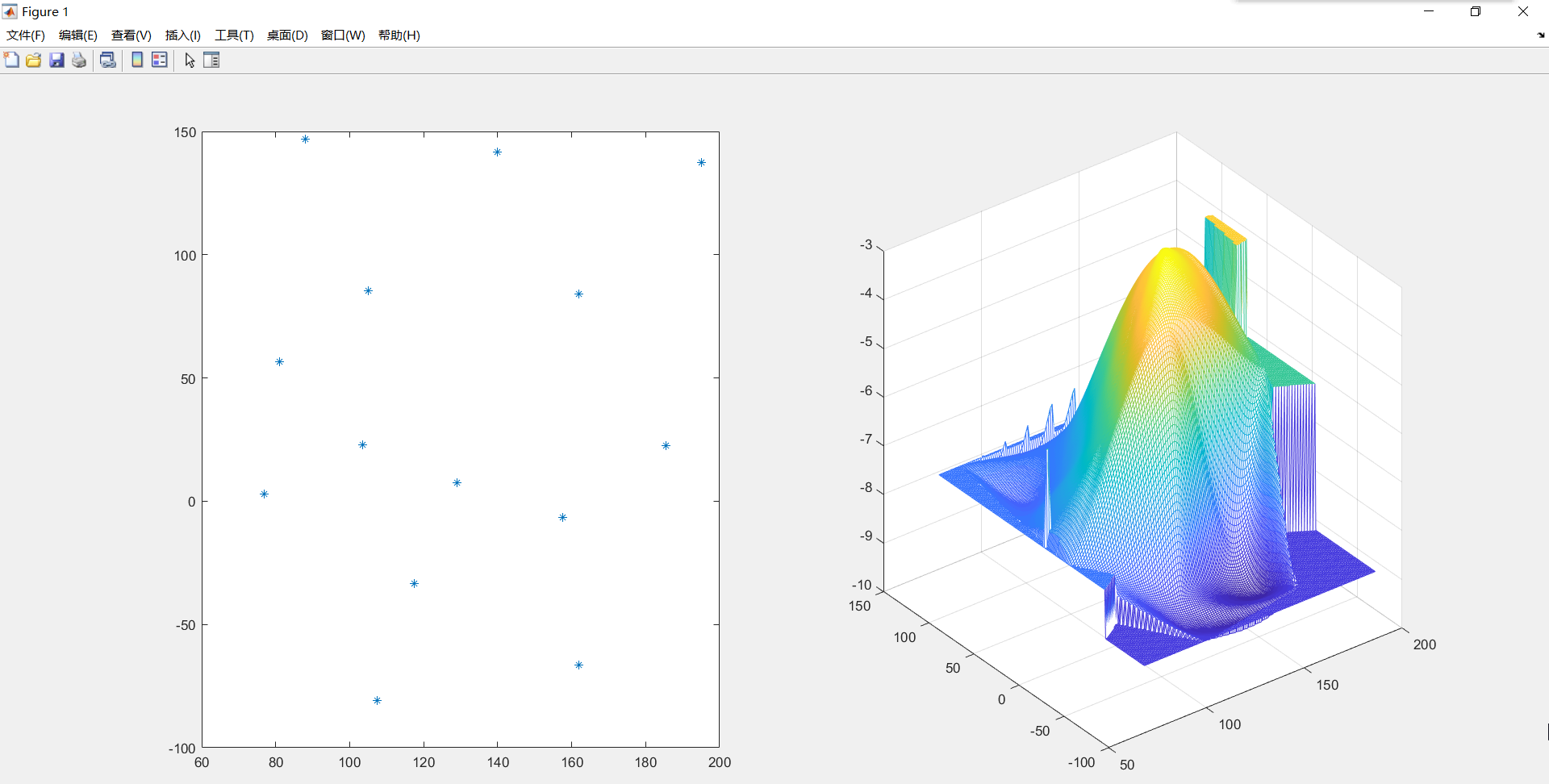
(2) 海底水深

format compact;
% 二维海底水深数据
clc,clear;
x=[129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5];
y=[7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5];
z=-[4,8,6,8,6,8,8,9,9,8,8,9,4,9]
xmm=minmax(x); % 求x的最大值和最小值
ymm=minmax(y); % 求y的最大值和最小值
xi=xmm(1):xmm(2);
yi=ymm(1):ymm(2);
zi1=griddata(x,y,z,xi,yi','cubic'); % 立方插值
zi2=griddata(x,y,z,xi,yi','nearest'); % 最近点插值
zi=zi1 %立方插值和最近点插值的混合插值的初始值
zi(isnan(zi1)) = zi2(isnan(zi1)); % 把立方插值中的不确定值缓存最近点插值的结果
subplot(1,2,1),plot(x,y,'*');
subplot(1,2,2),mesh(xi,yi,zi);

3.拟合

(1) 最小二乘拟合

x=[19     25    31     38    44]';
y=[19.0   32.3   49.0   73.3   97.8]';
r=[ones(5,1),x.^2]
ab=ry
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'o',x0,y0,'r')
%   y = 0.9726 +   0.0500*x^2
  

(2) 多项式拟合

x0=[1990  1991  1992  1993  1994  1995  1996];
y0=[70   122   144   152   174   196   202];
plot(x0,y0,'*')
a=polyfit(x0,y0,1)
y97=polyval(a,1997) % 拟合的多项式在1997处的值
y98=polyval(a,1998)

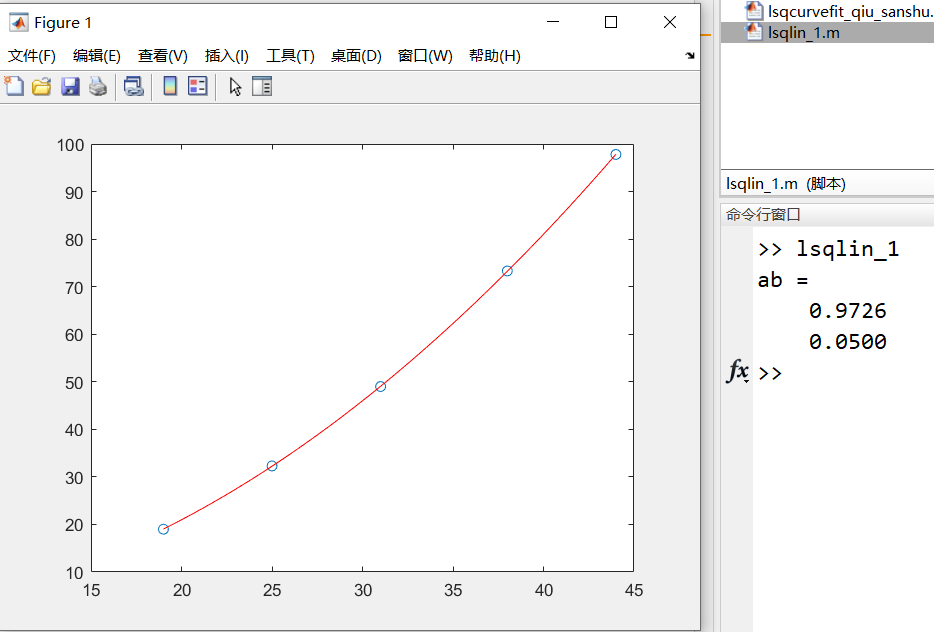
(3) 最小二乘优化lsqlin函数

x=[19     25    31     38    44]';
y=[19.0   32.3   49.0   73.3   97.8]';
r=[ones(5,1),x.^2];
ab=lsqlin(r,y)
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'o',x0,y0,'r')

 (4) 最小二乘优化lsqcurvefit函数，拟合函数中的参数

fun1.m

function f=fun1(canshu,xdata);
f= exp(-canshu(1)*xdata(:,1)).*sin(canshu(2)*xdata(:,2))+xdata(:,3).^2;  %其中canshu(1)=k1，canshu(2)=k2，注意函数中自变量的形式

data1.txt

1	15.02	23.73	5.49	1.21	14	15.94	23.52	5.18	1.98
2	12.62	22.34	4.32	1.35	15	14.33	21.86	4.86	1.59
3	14.86	28.84	5.04	1.92	16	15.11	28.95	5.18	1.37
4	13.98	27.67	4.72	1.49	17	13.81	24.53	4.88	1.39
5	15.91	20.83	5.35	1.56	18	15.58	27.65	5.02	1.66
6	12.47	22.27	4.27	1.50	19	15.85	27.29	5.55	1.70
7	15.80	27.57	5.25	1.85	20	15.28	29.07	5.26	1.82
8	14.32	28.01	4.62	1.51	21	16.40	32.47	5.18	1.75
9	13.76	24.79	4.42	1.46	22	15.02	29.65	5.08	1.70
10	15.18	28.96	5.30	1.66	23	15.73	22.11	4.90	1.81
11	14.20	25.77	4.87	1.64	24	14.75	22.43	4.65	1.82
12	17.07	23.17	5.80	1.90	25	14.35	20.04	5.08	1.53
13	15.40	28.57	5.22	1.66					

主函数

% 拟合函数y=e^(-k1*x1)*sin(k2*x2)+x3*3中的参数k1,k2
clc, clear
a=textread('data1.txt');
y0=a(:,[2,7]); %提出因变量y的数据
y0=nonzeros(y0); %去掉最后的零元素，且变成列向量
x0=[a(:,[3:5]);a([1:end-1],[8:10])]; %由分块矩阵构造因变量数据的2列矩阵
canshu0=rand(2,1); %拟合参数的初始值是任意取的
%非线性拟合的答案是不唯一的，下面给出拟合参数的上下界，
lb=zeros(2,1); %这里是随意给的拟合参数的下界,无下界时，默认值是空矩阵[]
ub=[20;2]; %这里是随意给的上界，无上界时，默认值是空矩阵[]
canshu=lsqcurvefit(@fun1,canshu0,x0,y0,lb,ub)  

Local minimum possible.

lsqcurvefit stopped because the final change in the sum of squares relative to 
its initial value is less than the default value of the function tolerance.

<stopping criteria details>


canshu =

    0.0000
    1.5483