Python 元胞自动机模拟——生命游戏

简介
元胞自动机（cellular automata) 是离散而抽象的计算系统。元胞自动机在时间和空间上是离散的，最小单位是简单元胞（单元格）。每个元胞会产生有限数量的状态集，后续元胞由其邻域元胞的状态确定。这里所说的领域元胞，是指当前元胞的前一个元胞(记作元胞A)以及元胞A左右两个元胞。也就是说，邻域元胞总共包含三个元胞。给定初始层的状态，基于一定规则，我们可以不断更新下一层元胞的状态。通俗的讲，元胞自动机就是基于一定规则的“繁衍机器”。

最简单的例子
这里，我们选取的元胞状态只有两种，分别为 0 和 1。每一层由 64 个元胞组成，若元胞状态为 1，那么控制台将打印星号(*)；如果元胞状态为 0，那么控制台将打印连字符(-)。也就是说，每一行由 64 个混合星号与连字符的图案组成。
那么，我们如何确定每一行的状态呢？

首先，我们要对第一行进行初始化操作。我们设置第 31 个元胞的状态为 1、其余 63 个元胞的状态为 0.
状态更新规则：若当前元胞的前一个元胞的状态为 1，或者前一个元胞的左右两边的元胞的状态有且只有一个值为 1， 那么该元胞的状态就为 1。反之，元胞的状态设为 0。对于第一列和最后一列，我们只需分别考虑右元胞和左元胞即可。对于中间部分的元胞来说，若其领域元胞的状态为[0,1,0]、[0,0,1]、[1,0,0]、[1,1,0]等状态时，当前元胞的状态就为 1。
代码

"""
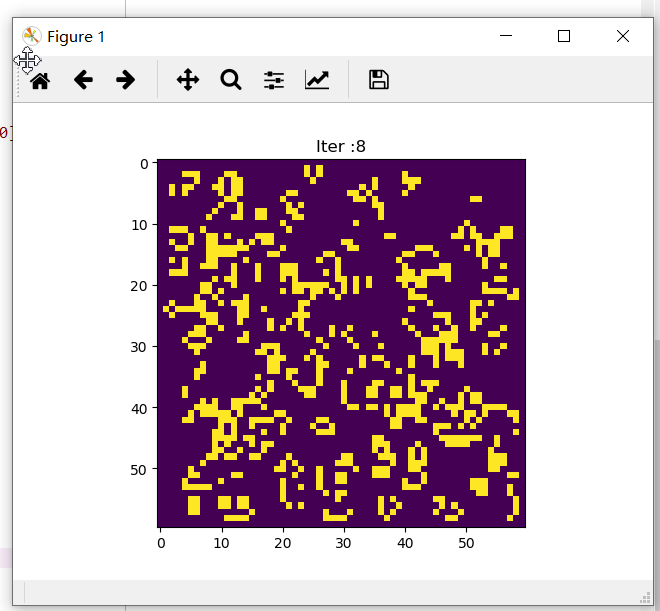
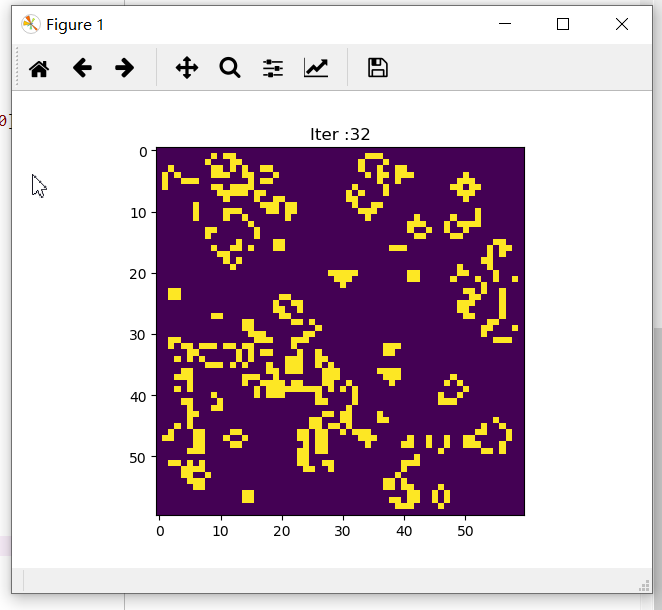
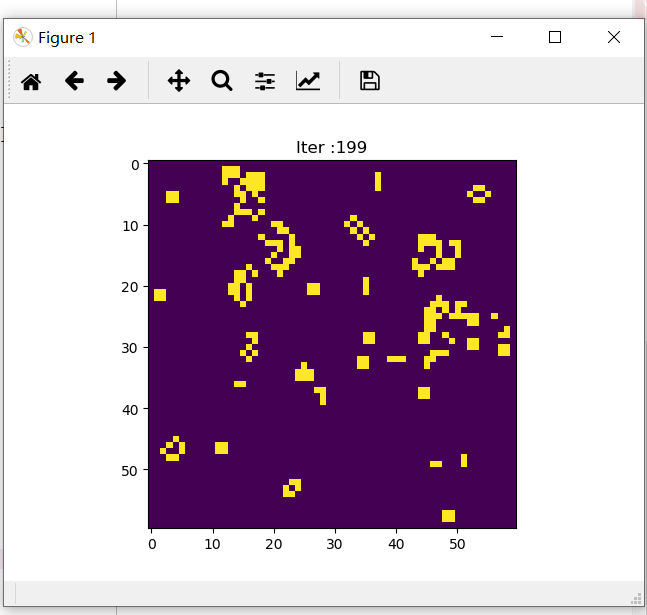
元胞自动机 Python 实现
"""
import numpy as np
import matplotlib.pyplot as plt
 
 
class GameOfLife(object):
 
  def __init__(self, cells_shape):
    """
    Parameters
    ----------
    cells_shape : 一个元组，表示画布的大小。
 
    Examples
    --------
    建立一个高20，宽30的画布
    game = GameOfLife((20, 30))
     
    """
 
    # 矩阵的四周不参与运算
    self.cells = np.zeros(cells_shape)
 
    real_width = cells_shape[0] - 2
    real_height = cells_shape[1] - 2
     
    self.cells[1:-1, 1:-1] = np.random.randint(2, size=(real_width, real_height))
    self.timer = 0
    self.mask = np.ones(9)
    self.mask[4] = 0
   
  def update_state(self):
    """更新一次状态"""
    buf = np.zeros(self.cells.shape)
    cells = self.cells
    for i in range(1, cells.shape[0] - 1):
      for j in range(1, cells.shape[0] - 1):
        # 计算该细胞周围的存活细胞数
        neighbor = cells[i-1:i+2, j-1:j+2].reshape((-1, ))
        neighbor_num = np.convolve(self.mask, neighbor, 'valid')[0]
        if neighbor_num == 3:
          buf[i, j] = 1
        elif neighbor_num == 2:
          buf[i, j] = cells[i, j]
        else:
          buf[i, j] = 0
    self.cells = buf
    self.timer += 1
   
  def plot_state(self):
    """画出当前的状态"""
    plt.title('Iter :{}'.format(self.timer))
    plt.imshow(self.cells)
    plt.show()
 
  def update_and_plot(self, n_iter):
    """更新状态并画图
    Parameters
    ----------
    n_iter : 更新的轮数
    """
    plt.ion()
    for _ in range(n_iter):
      plt.title('Iter :{}'.format(self.timer))
      plt.imshow(self.cells)
      self.update_state()
      plt.pause(0.2)
    plt.ioff()
           
 
if __name__ == '__main__':
  game = GameOfLife(cells_shape=(60, 60))
  game.update_and_plot(200)