#!/usr/bin/env python3 # -*- coding: utf-8 -*- from numpy import * def loadDataSet(): return [['a', 'c', 'e'], ['b', 'd'], ['b', 'c'], ['a', 'b', 'c', 'd'], ['a', 'b'], ['b', 'c'], ['a', 'b'], ['a', 'b', 'c', 'e'], ['a', 'b', 'c'], ['a', 'c', 'e']] def createC1(dataSet): C1 = [] for transaction in dataSet: for item in transaction: if not [item] in C1: C1.append([item]) C1.sort() # 映射为frozenset唯一性的,可使用其构造字典 return list(map(frozenset, C1)) # 从候选K项集到频繁K项集(支持度计算) def scanD(D, Ck, minSupport): ssCnt = {} for tid in D: for can in Ck: if can.issubset(tid): if not can in ssCnt: ssCnt[can] = 1 else: ssCnt[can] += 1 numItems = float(len(D)) retList = [] supportData = {} for key in ssCnt: support = ssCnt[key] / numItems if support >= minSupport: retList.insert(0, key) supportData[key] = support return retList, supportData def calSupport(D, Ck, min_support): dict_sup = {} for i in D: for j in Ck: if j.issubset(i): if not j in dict_sup: dict_sup[j] = 1 else: dict_sup[j] += 1 sumCount = float(len(D)) supportData = {} relist = [] for i in dict_sup: temp_sup = dict_sup[i] / sumCount if temp_sup >= min_support: relist.append(i) supportData[i] = temp_sup # 此处可设置返回全部的支持度数据(或者频繁项集的支持度数据) return relist, supportData # 改进剪枝算法 def aprioriGen(Lk, k): # 创建候选K项集 ##LK为频繁K项集 retList = [] lenLk = len(Lk) for i in range(lenLk): for j in range(i + 1, lenLk): L1 = list(Lk[i])[:k - 2] L2 = list(Lk[j])[:k - 2] L1.sort() L2.sort() if L1 == L2: # 前k-1项相等,则可相乘,这样可防止重复项出现 # 进行剪枝(a1为k项集中的一个元素,b为它的所有k-1项子集) a = Lk[i] | Lk[j] # a为frozenset()集合 a1 = list(a) b = [] # 遍历取出每一个元素,转换为set,依次从a1中剔除该元素,并加入到b中 for q in range(len(a1)): t = [a1[q]] tt = frozenset(set(a1) - set(t)) b.append(tt) t = 0 for w in b: # 当b(即所有k-1项子集)都是Lk(频繁的)的子集,则保留,否则删除。 if w in Lk: t += 1 if t == len(b): retList.append(b[0] | b[1]) return retList def apriori(dataSet, minSupport=0.2): C1 = createC1(dataSet) D = list(map(set, dataSet)) # 使用list()转换为列表 L1, supportData = calSupport(D, C1, minSupport) L = [L1] # 加列表框,使得1项集为一个单独元素 k = 2 while (len(L[k - 2]) > 0): Ck = aprioriGen(L[k - 2], k) Lk, supK = scanD(D, Ck, minSupport) # scan DB to get Lk supportData.update(supK) L.append(Lk) # L最后一个值为空集 k += 1 del L[-1] # 删除最后一个空集 return L, supportData # L为频繁项集,为一个列表,1,2,3项集分别为一个元素。 # 生成集合的所有子集 def getSubset(fromList, toList): for i in range(len(fromList)): t = [fromList[i]] tt = frozenset(set(fromList) - set(t)) if not tt in toList: toList.append(tt) tt = list(tt) if len(tt) > 1: getSubset(tt, toList) def calcConf(freqSet, H, supportData, ruleList, minConf=0.7): for conseq in H: conf = supportData[freqSet] / supportData[freqSet - conseq] # 计算置信度 # 提升度lift计算lift = p(a & b) / p(a)*p(b) lift = supportData[freqSet] / (supportData[conseq] * supportData[freqSet - conseq]) if conf >= minConf and lift > 1: print(freqSet - conseq, '-->', conseq, '支持度', round(supportData[freqSet - conseq], 2), '置信度:', conf, 'lift值为:', round(lift, 2)) ruleList.append((freqSet - conseq, conseq, conf)) # 生成规则 def gen_rule(L, supportData, minConf=0.7): bigRuleList = [] for i in range(1, len(L)): # 从二项集开始计算 for freqSet in L[i]: # freqSet为所有的k项集 # 求该三项集的所有非空子集,1项集,2项集,直到k-1项集,用H1表示,为list类型,里面为frozenset类型, H1 = list(freqSet) all_subset = [] getSubset(H1, all_subset) # 生成所有的子集 calcConf(freqSet, all_subset, supportData, bigRuleList, minConf) return bigRuleList if __name__ == '__main__': dataSet = loadDataSet() L, supportData = apriori(dataSet, minSupport=0.2) rule = gen_rule(L, supportData, minConf=0.7)
运行结果:
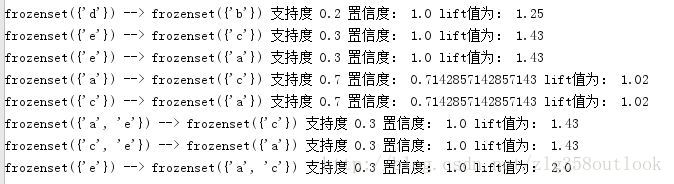
目录:
1.关联分析 返回目录
关联分析是一种在大规模数据集中寻找有趣关系的任务。这种关系表现为两种形式:
1.频繁项集(frequency item sets):经常同时出现的一些元素的集合;
2.关联规则(association rules): 意味着两种元素之间存在很强的关系。
下面举例来说明上面的两个概念:
| 交易号码 | 商品 |
| 0 | 豆奶, 莴苣 |
| 1 | 莴苣,尿布,葡萄酒,甜菜 |
| 2 | 莴苣,尿布,葡萄酒,橙汁 |
| 3 | 莴苣,豆奶,尿布,葡萄酒 |
| 4 | 莴苣,豆奶,尿布,橙汁 |
频繁项集是指经常出现在一起的元素的集合,上表中的集合 {葡萄酒,尿布,豆奶} 就是频繁项集的一个例子。同样可以找到如 “尿布 --> 葡萄酒”的关联规则,意味着如果有人买了尿布,就很可能也会买葡萄酒。使用频繁项集和关联规则,商家可以更好地理解顾客的消费行为,所以大部分关联规则分析示例来自零售业。
理解关联分析首先需要搞清楚下面三个问题:
1.如何定义这些有用的关系?
2.这些关系的强弱程度又是如何定义?
3.频繁的定义是什么?
要回答上面的问题,最重要的是理解两个概念:支持度和可信度。
支持度:一个项集的支持度(support)被定义为数据集中包含该项集的记录占总记录的比例。从表1 可以看出 项集 {豆奶} 的支持度为 4/54/5; 而在 5 条交易记录中 3 条包含 {豆奶,尿布},因此 {豆奶,尿布} 的支持度为 3/53/5.
可信度或置信度(confidence):是针对一条诸如尿布−−>葡萄酒尿布−−>葡萄酒的关联规则来定义的,这条规则的可信度被定义为“ 支持度({尿布,葡萄酒}) / 支持度({尿布})”。在表1 中可以发现 {尿布,葡萄酒} 的支持度是 3/53/5, {尿布} 的支持度为 4/54/5, 所以关联规则 “尿布 --> 葡萄酒”的可信度为 3/4=0.753/4=0.75, 意思是对于所有包含 "尿布"的记录中,该关联规则对其中的 75% 记录都适用。
2. Apriori 原理 返回目录
假设经营了一家杂货店,于是我们对那些经常在一起购买的商品非常感兴趣。假设我们只有 4 种商品:商品0,商品1,商品 2,商品3. 那么如何得可能被一起购买的商品的组合?
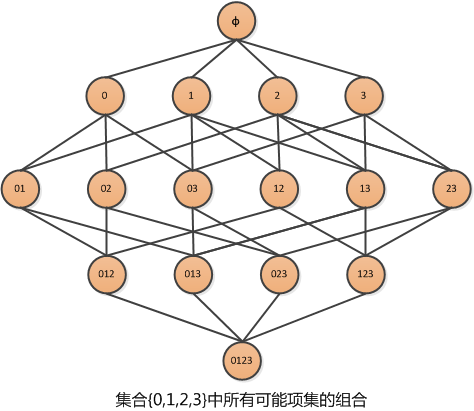
上图显示了物品之间所有可能的组合,从上往下一个集合是 ØØ,表示不包含任何物品的空集,物品集合之间的连线表明两个或者更多集合可以组合形成一个更大的集合。
我们的目标是找到经常在一起购买的物品集合。这里使用集合的支持度来度量其出现的频率。一个集合出现的支持度是指有多少比例的交易记录包含该集合。例如,对于上图,要计算 0,30,3 的支持度,直接的想法是遍历每条记录,统计包含有 00 和 33 的记录的数量,使用该数量除以总记录数,就可以得到支持度。而这只是针对单个集合 0,30,3. 要获得每种可能集合的支持度就需要多次重复上述过程。对于上图,虽然仅有4中物品,也需要遍历数据15次。随着物品数目的增加,遍历次数会急剧增加,对于包含 NN 种物品的数据集共有 2N−12N−1 种项集组合。所以即使只出售 100100 种商品的商店也会有 1.26×10301.26×1030 中可能的组合。计算量太大。
为了降低计算时间,研究人员发现了 AprioriApriori 原理,可以帮我们减少感兴趣的频繁项集的数目。
AprioriApriori 的原理:如果某个项集是频繁项集,那么它所有的子集也是频繁的。
即如果 {0,1} 是频繁的,那么 {0}, {1} 也一定是频繁的。
这个原理直观上没有什么用,但是反过来看就有用了,也就是说如果一个项集是非频繁的,那么它的所有超集也是非频繁的。如下图所示:

3. 使用 Apriori 算法来发现频繁集 返回目录
上面提到,关联分析的两个目标:发现频繁项集和发现关联规则。首先需要找到频繁项集,然后根据频繁项集获得关联规则。首先来讨论发现频繁项集。Apriori 是发现频繁项集的一种方法。
首先会生成所有单个物品的项集列表;
扫描交易记录来查看哪些项集满足最小支持度要求,那些不满足最小支持度的集合会被去掉;
对剩下的集合进行组合以生成包含两个元素的项集;
接下来重新扫描交易记录,去掉不满足最小支持度的项集,重复进行直到所有项集都被去掉。
数据集扫描的伪代码:
对数据集中的每条交易记录tran:
对每个候选项集can:
检查一下can是否是tran的子集:
如果是,则增加can的计数值
对每个候选项集:
如果其支持度不低于最低值,则保留
返回所有频繁项集列表