...Once upon a time a man came to the sea. The sea was stormy and dark. The man started to call for the little mermaid to appear but alas, he only woke up Cthulhu...
Whereas on the other end of the world Pentagon is actively collecting information trying to predict the monster's behavior and preparing the secret super weapon. Due to high seismic activity and poor weather conditions the satellites haven't yet been able to make clear shots of the monster. The analysis of the first shot resulted in an undirected graph with n vertices and m edges. Now the world's best minds are about to determine whether this graph can be regarded as Cthulhu or not.
To add simplicity, let's suppose that Cthulhu looks from the space like some spherical body with tentacles attached to it. Formally, we shall regard as Cthulhu such an undirected graph that can be represented as a set of three or more rooted trees, whose roots are connected by a simple cycle.
It is guaranteed that the graph contains no multiple edges and self-loops.

The first line contains two integers — the number of vertices n and the number of edges m of the graph (1 ≤ n ≤ 100, 0 ≤ m ≤ 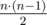 ).
).
Each of the following m lines contains a pair of integers x and y, that show that an edge exists between vertices x and y(1 ≤ x, y ≤ n, x ≠ y). For each pair of vertices there will be at most one edge between them, no edge connects a vertex to itself.
Print "NO", if the graph is not Cthulhu and "FHTAGN!" if it is.
题意:所有给定的点和边形成一个连通图,至少存在三个有根树, 且树的根形成一个环;
题解:
- 因为没有重边和自环,因此只要形成一个环就至少有三个点,而三个点就可以
- 分割成三棵有根树。因此只要满足图是联通的且存在环就满足题意。
- 可以用并查集检查是否联通,如果联通且存在环则必定有点数等于边数。
1 #include<bits/stdc++.h> 2 using namespace std; 3 int par[102]; 4 int find(int x) 5 { 6 if(par[x]==x)return x; 7 return par[x]=find(par[x]); 8 } 9 void unite(int x,int y) 10 { 11 x=find(x);y=find(y); 12 if(x!=y)par[x]=y; 13 } 14 int main() 15 { 16 int n,m;scanf("%d%d",&n,&m); 17 for(int i=0;i<101;i++)par[i]=i; 18 for(int i=0;i<m;i++) 19 { 20 int x,y;scanf("%d%d",&x,&y); 21 unite(x,y); 22 } 23 bool bb=1; 24 for(int i=2;i<=n;i++) 25 if(find(1)!=find(i))bb=0; 26 if(n!=m)bb=0; 27 if(bb)printf("FHTAGN! "); 28 else printf("NO "); 29 return 0; 30 }
灵活的数据管理和展示javascript类库 Recline.js
分享23款使用纯CSS3生成的知名logo设计
支持响应式布局的超棒颜色选择器 colorjoe
兄弟割席:HTML5标准制定组织分裂
30个绝对让你惊叹的幽默创意广告设计
免费图标素材:47套最新的超棒免费图标集
使用java的html解析器jsoup和jQuery实现一个自动重复抓取任意网站页面指定元素的web应用
免费素材下载:一套漂亮的卡通UI界面
分享10个超赞的画布Canvas,SVG和CSS3相关的jQuery插件