4 Values whose Sum is 0
| Time Limit: 15000MS | Memory Limit: 228000K | |
| Total Submissions: 25675 | Accepted: 7722 | |
| Case Time Limit: 5000MS | ||
Description
The SUM problem can be formulated as follows: given four lists A, B, C, D of integer values, compute how many quadruplet (a, b, c, d ) ∈ A x B x C x D are such that a + b + c + d = 0 . In the following, we assume that all lists have the same size n .
Input
The first line of the input file contains the size of the lists n (this value can be as large as 4000). We then have n lines containing four integer values (with absolute value as large as 228 ) that belong respectively to A, B, C and D .
Output
For each input file, your program has to write the number quadruplets whose sum is zero.
Sample Input
6 -45 22 42 -16 -41 -27 56 30 -36 53 -37 77 -36 30 -75 -46 26 -38 -10 62 -32 -54 -6 45
Sample Output
5
Hint
Sample Explanation: Indeed, the sum of the five following quadruplets is zero: (-45, -27, 42, 30), (26, 30, -10, -46), (-32, 22, 56, -46),(-32, 30, -75, 77), (-32, -54, 56, 30).
Source
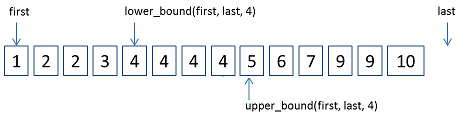
ForwardIter lower_bound(ForwardIter first, ForwardIter last,const _Tp& val)算法返回一个非递减序列[first, last)中的第一个大于等于值val的位置。
ForwardIter upper_bound(ForwardIter first, ForwardIter last, const _Tp& val)算法返回一个非递减序列[first, last)中第一个大于val的位置。
lower_bound和upper_bound如下图所示:
题意:
给定各有n个整数的四个数列A、B、C、D。要从每个数列中各取出1个数,使四个数的和为0。求出这样的组合的个数。当一个数列中有多个相同的数字时,把它们作为不同的数字看待。
分析:
所有全都判断一遍不可行。不过将它们对半分成AB和CD再考虑,就可以快速解决了。从2个数列中选择的话只有n2种组合,所以可以进行枚举。先从A、B中取出a、b后,为了使总和为0则需要从C、D中取出c + d = a - b。因此先将从C、D中取数字的n2种方法全部枚举出来,将这些和排好序,这样就可以运用二分搜索了。
1 #include <cstdio> 2 #include <algorithm> 3 using namespace std; 4 typedef long long ll; 5 const int maxn = 4000 + 10; 6 7 int n; 8 ll a[maxn], b[maxn], c[maxn], d[maxn]; 9 ll cd[maxn * maxn]; //C和D中数字的组合方法 10 11 void solve() 12 { 13 //枚举从C和D中取出数字的所有方法 14 for (int i = 0; i < n; i++) 15 { 16 for (int j = 0; j < n; j++) 17 { 18 cd[i * n + j] = c[i] + d[j]; 19 } 20 } 21 sort(cd, cd + n * n); 22 23 ll res = 0; 24 for (int i = 0; i < n; i++) 25 { 26 for (int j = 0; j < n; j++) 27 { 28 int CD = -(a[i] + b[j]); 29 //取出C和D中和为CD的部分 30 //二分搜索 31 res += upper_bound(cd, cd + n * n, CD) - lower_bound(cd, cd + n * n, CD);// 可能有多个答案 32 //lower_bound(first, last, const _Tp& val)算法返回一个非递减序列[first, last)中的第一个大于等于值val的位置。 33 //upper_bound(first, last, const _Tp& val)算法返回一个非递减序列[first, last)中第一个大于val的位置。 34 } 35 } 36 printf("%lld ", res); 37 } 38 39 int main() 40 { 41 scanf("%d", &n); 42 for (int i = 0; i < n; i++) 43 { 44 scanf("%lld%lld%lld%lld", &a[i], &b[i], &c[i], &d[i]); 45 } 46 solve(); 47 return 0; 48 }