斐波那契数列即为F(n)=F(n-1)+F(n-2),如1、1、2、3、5、8、13...
在计算的时候,通过最简单的递归计算,时间的复杂度是O(2N)
还有一个就是循环的一直计算的方法,时间的复杂度是O(N)
最小的时间复杂度的计算的方法是O(logN),这是因为这个函数是一个二阶递推数列,即这几个数据都是和前面的两个数据有关系的,这样的关系都可以用(F(n),F(n-1))=(F(n-1),F(n-2))×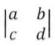 的公式进行表达,然后可以求出四个未知数。如果是三阶的递推数列,这个就是3×3的矩阵。最后(F(n),F(n-1))=(F(1),F(2))×
的公式进行表达,然后可以求出四个未知数。如果是三阶的递推数列,这个就是3×3的矩阵。最后(F(n),F(n-1))=(F(1),F(2))×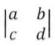 的n-2次方,在求方的时候,也有快捷的方式,比如10的75次方,75的二进制数是1001011,就是75=64+8+2+1,即1075=1064×108×102×101,这样就可以大大的缩短计算的时间。
的n-2次方,在求方的时候,也有快捷的方式,比如10的75次方,75的二进制数是1001011,就是75=64+8+2+1,即1075=1064×108×102×101,这样就可以大大的缩短计算的时间。