Codeforces 687B. Remainders Game[剩余]

B. Remainders Game

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Today Pari and Arya are playing a game called Remainders.

Pari chooses two positive integer x and k, and tells Arya k but not x. Arya have to find the value 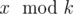. There are n ancient numbers c1, c2, ..., cn and Pari has to tell Arya  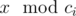if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value  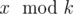for any positive integer x?

Note, that 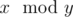 means the remainder of x after dividing it by y.

Input

The first line of the input contains two integers n and k (1 ≤ n,  k ≤ 1 000 000) — the number of ancient integers and value k that is chosen by Pari.

The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 1 000 000).

Output

Print "Yes" (without quotes) if Arya has a winning strategy independent of value of x, or "No" (without quotes) otherwise.

Examples

input

4 5
2 3 5 12

output

Yes

input

2 7
2 3

output

No

Note

In the first sample, Arya can understand 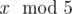 because 5 is one of the ancient numbers.

In the second sample, Arya can't be sure what 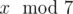 is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.

---

题意：有数字x和k，x未知；知道x mod ci的结果，问x mod k是否唯一

---

官方题解：

Hint

Assume the answer of a test is No. There must exist a pair of integers x1 and x2 such that both of them have the same remainders after dividing by any ci, but they differ in remainders after dividing by k. Find more facts about x1 and x2!

Solution

Consider the x1 and x2 from the hint part. We have x1 - x2 ≡ 0 (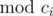) for each 1 ≤ i ≤ n. 

So:

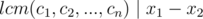
We also have 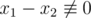 (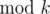). As a result:

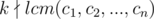
We've found a necessary condition. And I have to tell you it's also sufficient!

Assume 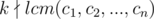, we are going to prove there exists x1, x2 such that x1 - x2 ≡ 0 (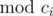) (for each 1 ≤ i ≤ n), and  (). 

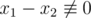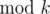A possible solution is x1 = lcm(c1, c2, ..., cn) and x2 = 2 × lcm(c1, c2, ..., cn), so the sufficiency is also proved.

So you have to check if lcm(c1, c2, ..., cn) is divisible by k, which could be done using prime factorization of k and ci values.

For each integer x smaller than MAXC, find it's greatest prime divisor gpdx using sieve of Eratosthenes in .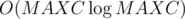 

Then using gpd array, you can write the value of each coin as p1q1p2q2...pmqm where pi is a prime integer and 1 ≤ qi holds. This could be done in 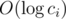 by moving from ci to  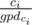and adding gpdci to the answer. And you can factorize k by the same way. Now for every prime p that 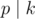, see if there exists any coin i that the power of p in the factorization of ci is not smaller than the power of p in the factorization of k.

Complexity is .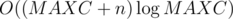

---

题解前一部分比较好，后面还用筛法太扯了，质因数分解不用判质数

假设有两个x1和x2,如果x mod k不唯一的话则x1和x2满足：

x1-x2≡0(mod ci)----->lcm(c1,c2,..,cn)|x1-x2

x1-x2!≡0(mod k)

那么：

最小的x1-x2就是lcm

代入得lcm!≡0(mod k) 也就是k!|lcm

质因数分解k判断每个质因子是否是某个ci 的约数，如果全是则可以整除，解唯一，一定可以猜出

//
//  main.cpp
//  cf687b
//
//  Created by Candy on 9/20/16.
//  Copyright © 2016 Candy. All rights reserved.
//

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e6+5;
int read(){
    char c=getchar();int x=0,f=1;
    while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0'; c=getchar();}
    return x*f;
}
int n,k,c[N];
bool check(int a){
    for(int i=1;i<=n;i++) if(c[i]%a==0) return 1;
    return 0;
}
int main(int argc, const char * argv[]) {
    n=read();k=read();
    for(int i=1;i<=n;i++) c[i]=read();
    for(int i=2;i<=k;i++){
        int a=1;
        while(k%i==0) a*=i,k/=i;
        if(a!=1&&!check(a)){printf("No");return 0;}
    }
    printf("Yes");
    return 0;
}