Codecraft-17 and Codeforces Round #391 (Div. 1 + Div. 2, combined)
23:35~2:35 1.12.2017 |实际 23:35~1:40
题意:妙蛙种子太神了
题解:妙蛙种子太神了

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> using namespace std; const int N=1e5+5,INF=1e9; int n,c[300],ans=INF; char s[N],a[20]="Bulbasaur"; int main(int argc, const char * argv[]) { scanf("%s",s+1); n=strlen(s+1); for(int i=1;i<=n;i++) c[s[i]]++; int len=strlen(a);//printf("ln %d %c ",len,a[0]); for(int i=0;i<len;i++) ans=min(ans,c[a[i]]); ans=min(ans,min(c['a']/2,c['u']/2)); printf("%d",ans); return 0; }
题意:选尽量多的数使他们的gcd不为1
题解:
gcd不为1一定有一个公共质因子
然后就是用那个避免线性筛的常用技巧
vis[i]表示i这个数出现次数,枚举这个公共质因子,再枚举他的所有倍数,用vis[倍数]更新质因子为他时的答案
根据枚举质因子的所有倍数复杂度为O(n) ,根据素数个数n/logn和调和级数

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> using namespace std; const int N=1e5+5; typedef long long ll; inline int read(){ char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int n,a,vis[N],mx; int p[N],notp[N]; void sieve(int n){ for(int i=2;i<=n;i++){ if(!notp[i]) p[++p[0]]=i; for(int j=1;j<=p[0]&&i*p[j]<=n;j++){ notp[i*p[j]]=1; if(i%p[j]==0) break; } } } void solve(int n){ int ans=0,tmp=0; for(int j=1;j<=p[0];j++){ tmp=0; for(int i=p[j];i<=n;i+=p[j]) if(vis[i]) tmp+=vis[i]; ans=max(ans,tmp);//printf("hi %d %d ",p[j],tmp); } printf("%d ",ans==0?1:ans); } int main(int argc, const char * argv[]){ //freopen("in.txt","r",stdin); n=read(); for(int i=1;i<=n;i++) a=read(),vis[a]++,mx=max(mx,a); sieve(mx); solve(mx); return 0; }
注意:没注意多个数相同WA一次,没特判一个数WA一次,i打成了a最终结果没过,SAD
貌似比标解用质因子分解要优吧,标解是O(n^3/2),翻了几页提交记录我好像是最快的哈哈哈
题意:自己看
题解:
一下子就想到了,在每个gym里都相同才可以互换,然后可以互换的求全排列再乘法原理
然后就开始想怎么求在每个gym里都相同,也许是太晚了想了一个多小时还不会
其实很简单,用一个vector数组储存每种type在那些gym里出现过,出现多次就保存多个
然后把这些vector排序,用离散化去重的方法统计答案就行了
vector也是按字典序比较的
这种保存出现位置的做法和这道题有点类似吧

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <vector> using namespace std; const int N=1e6+5,MOD=1e9+7; typedef long long ll; inline int read(){ char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int n,m; vector<int> v[N]; int main(){ //freopen("in.txt","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++){ int g=read(); while(g--) v[read()].push_back(i); } sort(v+1,v+1+m); ll _=1,ans=1; for(int i=2;i<=m;i++){ if(v[i]==v[i-1]) ans=(ans*(++_))%MOD; else _=1; } printf("%d",ans); }
D.Felicity's Big Secret Revealed
题意:一个01串分成k份使得每份形成的数字是连续的(可以重复)的方案数,求k=2...n+1的和
题解:
当时没认真想,确实想不出来,看了标解
竟然是状压DP,好吧这东西确实没练过要好好练一下了
首先发现这个数最大到20 (1*(1 bits) + 2*(2 bits) + 4*(3 bits) + 8*(4 bits) + 5*(5 bits) = 74 bits)
d[i][s]表示当前切了i次且已经有的数字的集合是s的方案数,枚举下一次切在哪转移就行了
可以k=2..n+1分别dp一次,但是可以发现这东西对切的次数其实就是没有限制(几次都可以啊),所以无论现在i是几一碰到是s合法的方案更新就行了
小技巧:判断s里是连续的可以 !(s&(s+1))
注意:一次里的数>20要break

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> using namespace std; const int N=77,INF=1e9,MOD=1e9+7; int n,All; char a[N]; int d[N][1<<20],ans; inline void mod(int &x){if(x>=MOD) x-=MOD;} void dp(){ for(int i=0;i<=n;i++){//printf("hi %d ",i); d[i][0]=1; for(int s=0;s<All;s++){ if(d[i][s]==0) continue;//printf("d %d %d %d ",i,s,d[i][s]); if(s&&!(s&(s+1))) mod(ans+=d[i][s]);//,printf("ans %d ",ans); int now=0; for(int j=i+1;j<=n;j++){ now=(now<<1)|(a[j]-'0');//now*2+s[i]-'0' if(now>20) break; if(now) mod(d[j][s|(1<<(now-1))]+=d[i][s]); } } } } int main(){ //freopen("in.txt","r",stdin); scanf("%d%s",&n,a+1);All=(1<<20); dp(); printf("%d",ans); }
题意:奇妙的函数
题解:
当时太困了睡觉了
后来从r到0倒推想了想没想出来 1也合法真是好烦啊
先考虑f0,f0(n)=x*(x-1)+x*1 x是p的质因子个数,显然是积性函数
然后 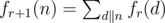
积性函数的约数和也是积性函数
但这里莫比乌斯反演显然没用
所以求fr(n)只要求∏fr(p^e)就可以了
fr(p^e)=Σ{i=0..e}fr-1(p^i) 与p是无关的与e有关
用dp d[i][j]=Σ{k=0..j}d[i-1][k]=d[i-1][k]+d[i][k-1] 即可
时间复杂度的主要瓶颈在求一个数的质因子分解上,学到一个好厉害的做法,线性筛的时候保存lp[i]为i的最小质因子然后直接用,比普通的枚举快了一倍

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> using namespace std; const int N=1e6+5,MOD=1e9+7; typedef long long ll; inline int read(){ char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int Q,n,r,d[N][21]; int notp[N],p[N],lp[N]; void sieve(int n){ for(int i=2;i<=n;i++){ if(!notp[i]) p[++p[0]]=i,lp[i]=i; for(int j=1;j<=p[0]&&i*p[j]<=n;j++){ notp[i*p[j]]=1;lp[i*p[j]]=p[j]; if(i%p[j]==0) break; } } } void dp(){ for(int i=1;i<=20;i++) d[0][i]=2; for(int i=1;i<N;i++){ d[i][0]=1; for(int j=1;j<=20;j++) d[i][j]=(d[i-1][j]+d[i][j-1])%MOD; } } void solve(int r,int n){//printf("sol %d %d ",r,n); ll ans=1; while(n!=1){ int e=0,p=lp[n]; while(n%p==0) n/=p,e++; ans=(ans*d[r][e])%MOD; } printf("%I64d ",ans); } int main(){ //freopen("in.txt","r",stdin); sieve(N-1); dp(); Q=read(); while(Q--){ r=read();n=read(); solve(r,n); } }
F 弃
G 弃
