方法一:
直接排序法,这是一种最直观最容易理解的方法,先将数组用某种方法进行排序,然后选取第k大的数,算法的好坏取决与排序算法,常见的排序有,冒泡排序(n^2),擦入排序(n^2),堆排序(nlgn),快速排序(nlgn),归并排序(nlgn),计数排序(n+k),基数排序(n),由于方法简单这里就不给出代码了。
方法二:
// find_kth.cpp : 定义控制台应用程序的入口点。
//方法类似于归并排序,平均时间复杂度O(n),最坏时间复杂度O(n^2)
#include "stdafx.h"
#include<iostream>
using namespace std;
int find_the_kth_num(int *a,int k,int front,int end){
int comp = a[front];
if(k > (end + 1)){
cout<<"数组越界!!"<<endl;
return -1;
}else{
if(front == end){
return a[front];
}else{
int i = front;
int j = front + 1;
for(;j <= end;++j){
if(a[j] < comp){
++i;
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
if(i == k - 1){
return comp;
}else{
a[front] = a[i];
a[i] = comp;
if(i < k - 1){
return find_the_kth_num(a,k,i + 1,end);
}else{
return find_the_kth_num(a,k,front,i - 1);
}
}
}
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[] = {1,2,3,5,6,7,8,9,4,5,6,7,8,9};
cout<<find_the_kth_num(a,8,0,13);
while(1);
return 0;
}
方法三:
最坏情况线性时间的选择法(原理部分转):
基本原理:
SELECT算法的思想是要保证对数组的划分是个好的划分,对PARTITION过程进行了修改。现在通过SELECT算法来确定n个元素的输入数组中的第i小的元素,具体操作步骤如下:
(1)将输入数组的n个元素划分为n/5(上取整)组,每组5个元素,且至多只有一个组有剩下的n%5个元素组成。
(2)寻找每个组织中中位数。首先对每组中的元素(至多为5个)进行插入排序,然后从排序后的序列中选择出中位数。
(3)对第2步中找出的n/5(上取整)个中位数,递归调用SELECT以找出其中位数x。(如果是偶数去下中位数)
(4)调用PARTITION过程,按照中位数x对输入数组进行划分。确定中位数x的位置k。
(5)如果i=k,则返回x。否则,如果i<k,则在地区间递归调用SELECT以找出第i小的元素,若干i>k,则在高区找第(i-k)个最小元素。
关于复杂度:设复杂度T(n)则:
T(n) <= T(n/5) + T(n/2+(n/2)*(2/5)) + O(n) <= T(n/5) + T(7n/5) + O(n)
容易的到:T(n) = O(n)
这里我们将讨论一个有意思的问题:为什么选5,选3行吗?
答案是肯定的:不行!!
分析:如果选3作为划分基准,那么
T(n) = T(n/3) + T(n/2+(n/2)*(n/3)) + O(n) <= T(n/3) + T(2n/3) + O(n) = O(nlgn)
(注意:这里我们用到了一个结论,对于T(n) <= T(an) + T(bn) +O(n),若a+b<1则T(n) = O(n)若a+b = 1则T(n) = O(nlgn))
实际上基准为7及其以上也是可以的
SELECT算法通过中位数进行划分,可以保证每次划分是对称的,这样就能保证最坏情况下运行时间为θ(n)。举个例子说明此过程,求集合A={32,23,12,67,45,78,10,39,9,58,125,84}的第5小的元素,操作过程如下图所示: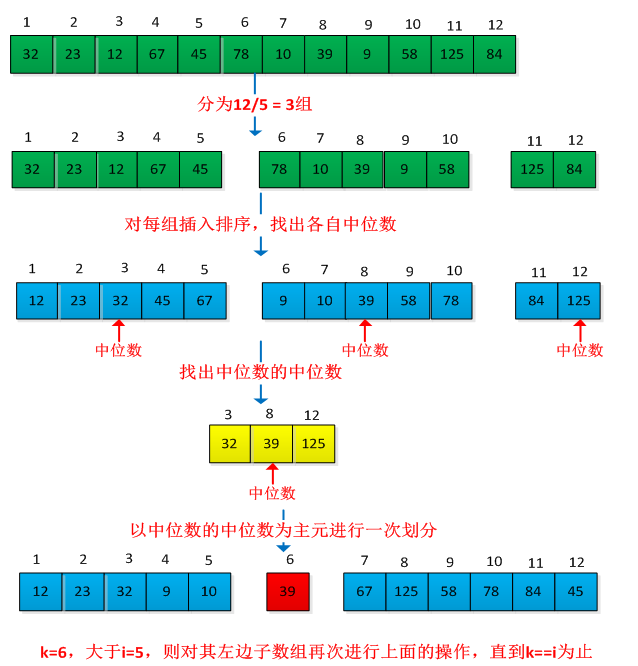
现在采用C语言实现上面的例子,完整程序如下所示:
/*Filename:select_middle_good.cpp */
/*从一个数组中选取第k大的数值并返回其值 */
/*思路: */
#include<iostream>
using namespace std;
int partition(int *Data,int front,int end,int com){//划分函数,一直数组起点终点 以及数组中的数com用com这个数作为划分点进行划分,左边的数都小于或等于com,右边的数都大于com
int i = front;
int j = front;
int temp = 0;
int mark = front;
for(;j < end;++j){
if(Data[j] <= com){
temp = Data[j];
Data[j] = Data[i];
Data[i] = temp;
if(Data[i] == com){//标记最后一次遇到与com值相等的数的交换后被放到的位置
mark = i;
}
++i;
}
}
--i;
temp = Data[i];
Data[i] = Data[mark];
Data[mark] = temp;
return i;
}
void sort(int *Data,int front,int end){//数组局部排序,冒泡法
int temp = 0;
if(end - front == 0)return;
for(int i = 0;i < (end - front + 1);++i){
for(int j = front;j < end - i;++j){
if(Data[j] > Data[j + 1]){
temp = Data[j];
Data[j] = Data[j + 1];
Data[j + 1] = temp;
}
}
}
}
int select(int *Data,int front,int end,int k){
cout<<front<<"--"<<end<<endl;//输出每次select函数被调用时数组的起点与终点
/*处理长度为5以内的数组*/
if((end - front) < 5){//数组长度不足5的时候,特殊处理
if(k > (end - front + 1)){
cout<<"越界!!!";
return -1;
}else{
sort(Data,front,end);
return Data[front + k -1];
}
}
int sub_len = (end - front + 1)/5;
int sub_len_a = (end - front + 1 - sub_len * 5) > 0?sub_len + 1:sub_len;
int *p = new int[sub_len_a];
for(int i = 0;i < sub_len;++i){
sort(Data,front + 5*i,5*i + 4);//数组每五个数字进行排序(冒泡法)
p[i] = Data[front + 5*i +2];
}
if(sub_len_a > sub_len){
p[sub_len_a - 1] = Data[front + 5*sub_len + 1]; //数组长度不是5的整数倍,中值序列最后一位取尾子数组第一个值(这是随意取的一个值 不回影响算法性能)
}
int com = select(p,0,sub_len_a - 1,sub_len_a/2);//递归选取中值的中值
int d = partition(Data,front,end,com);//用中值的中值作为划分边界进行一次划分,实属组左边的数值都小于该值,右边的值都大于该值
if(d == (k - 1)){
return Data[d];//划分值恰好是要查找的那个数
}else if(d < (k - 1)){
return select(Data,d + 1,end,k - (d - front + 1));//划分数位置左边的数个数小于要求值的位置
}else{
return select(Data,front,d - 1,k);//划分数位置大于要求值的位置
}
}
int main(){
int test[] = {7,3,2,6,5,4,2,1,9,11};
cout<<select(test,0,9,6)<<endl;
for(int i = 0;i <= 8;++i){
cout<<test[i]<<" ";
}
return 0;
}