第一部分 算法简单概念
- 算法概念
- 复习:递归
- 时间复杂度
- 空间复杂度
什么是算法?
- 算法(Algorithm):一个计算过程,解决问题的方法

复习:递归
- 递归的两个特点:
- 调用自身
- 结束条件
- 看下面几个函数:

递归:练习

时间复杂度
- 看代码:
-
- print('Hello World')
-
- for i in range(n):
- print('Hello World')
-
- for i in range(n):
- for j in range(n):
- print('Hello World')
-
- for i in range(n):
- for j in range(n):
- for k in range(n):
- print('Hello World')
1 上面四组代码,哪组运行时间最短? 2 用什么方式来体现代码(算法)运行的快慢?
- 类比生活中的一些事件,估计时间:
- 眨一下眼 一瞬间/几毫秒
- 口算“29+68” 几秒
- 烧一壶水 几分钟
- 睡一觉 几小时
- 完成一个项目 几天/几星期/几个月
- 飞船从地球飞出太阳系 几年
- 时间复杂度:用来评估算法运行效率的一个东西

- 那这些代码呢?

- 那这个代码呢?

- 时间复杂度-小结
- 时间复杂度是用来估计算法运行时间的一个式子(单位)。
- 一般来说,时间复杂度高的算法比复杂度低的算法慢。
- 常见的时间复杂度(按效率排序)
- O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)
- 不常见的时间复杂度(看看就好)
- O(n!) O(2n) O(nn) …
- 如何一眼判断时间复杂度?
- 循环减半的过程O(logn)
- 几次循环就是n的几次方的复杂度
空间复杂度
- 空间复杂度:用来评估算法内存占用大小的一个式子
- “空间换时间”
列表查找
- 列表查找:从列表中查找指定元素
- 输入:列表、待查找元素
- 输出:元素下标或未查找到元素
- 顺序查找
- 从列表第一个元素开始,顺序进行搜索,直到找到为止。
- 二分查找
- 从有序列表的候选区data[0:n]开始,通过对待查找的值与候选区中间值的比较,可以使候选区减少一半。
二分查找
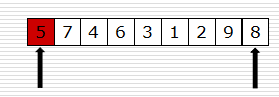
- 使用二分查找来查找3

列表查找-代码
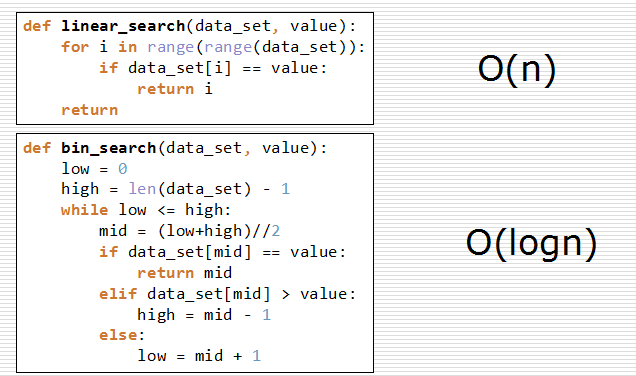
递归版本的二分查找
def bin_search_rec(data_set, value, low, high): if low <= high: mid = (low + high) // 2 if data_set[mid] == value: return mid elif data_set[mid] > value: return bin_search_rec(data_set, value, low, mid - 1) else: return bin_search_rec(data_set, value, mid + 1, high) else: return
列表查找:练习
- 现有一个学员信息列表(按id增序排列),格式为:
[ {id:1001, name:"张三", age:20}, {id:1002, name:"李四", age:25}, {id:1004, name:"王五", age:23}, {id:1007, name:"赵六", age:33} ]
- 修改二分查找代码,输入学生id,输出该学生在列表中的下标,并输出完整学生信息。
- Letcode
- 34. Search for a Range (二分查找升级版)
- 1. Two Sum
列表排序
- 列表排序
- 将无序列表变为有序列表
- 应用场景:
- 各种榜单
- 各种表格
- 给二分排序用
- 给其他算法用
- 输入:无序列表
- 输出:有序列表
- 升序与降序
- 排序low B三人组:
- 冒泡排序
- 选择排序
- 插入排序
- 快速排序
- 排序NB二人组:
- 堆排序
- 归并排序
- 没什么人用的排序:
- 基数排序
- 希尔排序
- 桶排序
排序Low B三人组
- 大家自己能想到怎么完成一次排序吗?
- 冒泡排序
- 选择排序
- 插入排序
- 算法关键点:
- 有序区
- 无序区
冒泡排序思路
- 首先,列表每两个相邻的数,如果前边的比后边的大,那么交换这两个数……
- 会发生什么?
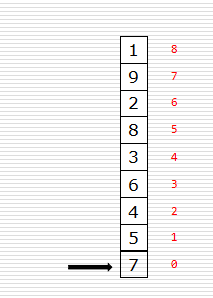
- 代码关键点:
- 趟
- 无序区
- 冒泡排序代码
def bubble_sort(li): for i in range(len(li)-1): for j in range(len(li)-i-1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j]
- 时间复杂度:O(n2)
- 冒泡排序-优化
- 如果冒泡排序中执行一趟而没有交换,则列表已经是有序状态,可以直接结束算法。
def bubbole_sort_1(li): for i in range(len(li)-1): exchange = False for j in range(len(li)-i-1): if li[j] > li[j+1]: li[j],li[j+1] = li[j+1],li[j] exchange = True if not exchange: return
- 选择排序思路
- 一趟遍历记录最小的数,放到第一个位置;
- 再一趟遍历记录剩余列表中最小的数,继续放置;
- ……
- 问题是:怎么选出最小的数?
- 代码关键点:
- 无序区
- 最小数的位置
- 选择排序代码
def select_sort(li): for i in range(len(li) - 1): min_loc = i for j in range(i+1, len(li)): if li[j] < li[min_loc]: min_loc = j if min_loc != i: li[i], li[min_loc] = li[min_loc], li[i]
- 时间复杂度:O(n2)
- 插入排序思路
- 列表被分为有序区和无序区两个部分。最初有序区只有一个元素。
- 每次从无序区选择一个元素,插入到有序区的位置,直到无序区变空。
- 代码关键点:
- 摸到的牌
- 手里的牌



1 def insert_sort(li): 2 for i in range(1, len(li)): 3 tmp = li[i] 4 j = i - 1 5 while j >= 0 and tmp < li[j]: 6 li[j + 1] = li[j] 7 j = j - 1 8 li[j + 1] = tmp
- 时间复杂度:O(n2)
- 优化空间:应用二分查找来寻找插入点(并没有什么卵用)
小结——排序LOW B三人组
- 冒泡排序 插入排序 选择排序
- 时间复杂度:O(n2)
- 空间复杂度:O(1)
快速排序
- 快速排序:快
- 好写的排序算法里最快的
- 快的排序算法里最好写的
- 快速排序思路
-
取一个元素p(第一个元素),使元素p归位;
-
列表被p分成两部分,左边都比p小,右边都比p大;
-
递归完成排序。
-
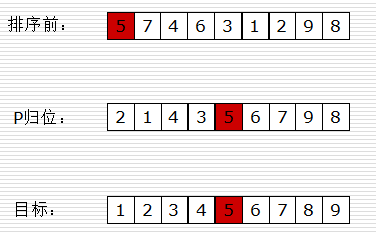
- 算法关键点:
- 整理
- 递归

1 def quick_sort(data, left, right): 2 if left < right: 3 mid = partition(data, left, right) 4 quick_sort(data, left, mid - 1) 5 quick_sort(data, mid + 1, right)
- 怎么写partition函数
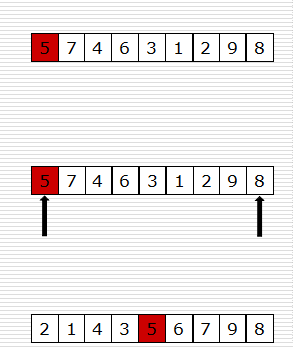

1 def partition(data, left, right): 2 tmp = data[left] 3 while left < right: 4 while left < right and data[right] >= tmp: 5 right -= 1 6 data[left] = data[right] 7 while left < right and data[left] <= tmp: 8 left += 1 9 data[right] = data[left] 10 data[left] = tmp 11 return left
还不理解partition函数?
def partition(data, left, right): tmp = data[left] while left < right: while left < right and data[right] >= tmp: right -= 1 data[left] = data[right] while left < right and data[left] <= tmp: left += 1 data[right] = data[left] data[left] = tmp return left
快速排序-如何
- 效率
- 快速排序真的比冒泡排序快吗?
- 为什么快了?
- 快了多少?
- 问题
- 最坏情况
- 递归
快速排序-练习
- 如果想将列表进行降序排序,应该修改哪些符号?
- 还是对于刚才那个学生信息表,修改快速排序代码,使其能够进行排序。
堆排序前传——树与二叉树简介
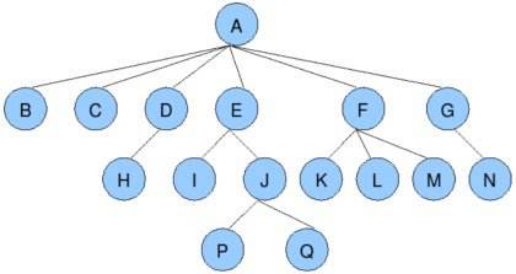
- 树是一种数据结构 比如:目录结构
- 树是一种可以递归定义的数据结构
- 树是由n个节点组成的集合:
- 如果n=0,那这是一棵空树;
- 如果n>0,那存在1个节点作为树的根节点,其他节点可以分为m个集合,每个集合本身又是一棵树。
- 一些概念
- 根节点、叶子节点
- 树的深度(高度)
- 树的度
- 孩子节点/父节点
- 子树
特殊且常用的树——二叉树
- 二叉树:度不超过2的树(节点最多有两个叉)

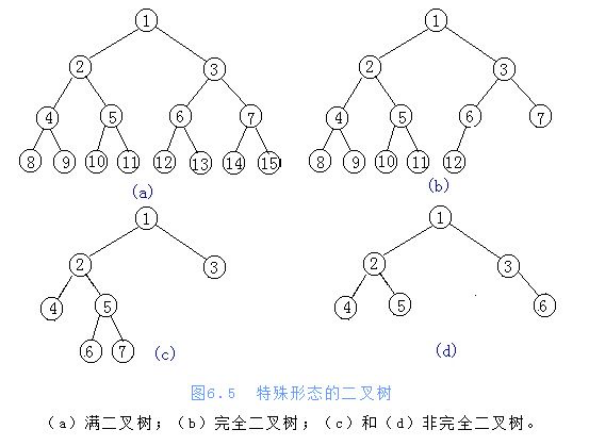
- 两种特殊二叉树
- 满二叉树
- 完全二叉树
- 二叉树的存储方式
-
- 链式存储方式
- 顺序存储方式(列表)
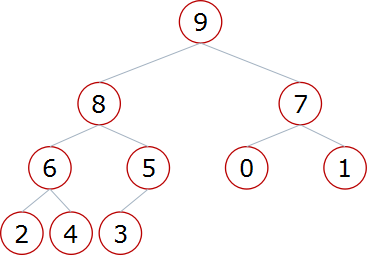
- 父节点和左孩子节点的编号下标有什么关系?
- 0-1 1-3 2-5 3-7 4-9
-
- i – 2i+1
- 父节点和右孩子节点的编号下标有什么关系?
- 0-2 1-4 2-6 3-8 4-10
-
i – 2i+2
- 比如,我们要找根节点左孩子的左孩子

二叉树小结
- 二叉树是度不超过2的树
- 满二叉树与完全二叉树
- (完全)二叉树可以用列表来存储,通过规律可以从父亲找到孩子或从孩子找到父亲
堆排序
- 堆
- 大根堆:一棵完全二叉树,满足任一节点都比其孩子节点大

- 小根堆:一棵完全二叉树,满足任一节点都比其孩子节点小

- 堆这个玩意…
- 假设:节点的左右子树都是堆,但自身不是堆

-
- 当根节点的左右子树都是堆时,可以通过一次向下的调整来将其变换成一个堆。
- 堆排序过程
-
建立堆
-
得到堆顶元素,为最大元素
-
去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序。
-
堆顶元素为第二大元素。
-
重复步骤3,直到堆变空。
-
- 构造堆
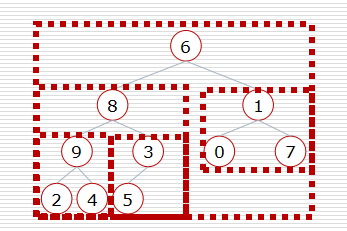
- 挨个出数

 堆排序代码
堆排序代码归并排序
- 假设现在的列表分两段有序,如何将其合成为一个有序列表
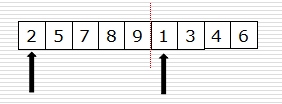
- 这种操作称为一次归并。

1 def merge(li, low, mid, high): 2 i = low 3 j = mid + 1 4 ltmp = [] 5 while i <= mid and j <= high: 6 if li[i] <= li[j]: 7 ltmp.append(li[i]) 8 i += 1 9 else: 10 ltmp.append(li[j]) 11 j += 1 12 while i <= mid: 13 ltmp.append(li[i]) 14 i += 1 15 while j <= high: 16 ltmp.append(li[j]) 17 j += 1 18 li[low:high + 1] = ltmp
有了归并怎么用?

- 分解:将列表越分越小,直至分成一个元素。
- 一个元素是有序的。
- 合并:将两个有序列表归并,列表越来越大。

def mergesort(li, low, high): if low < high: mid = (low + high) // 2 mergesort(li, low, mid) mergesort(li, mid + 1, high) merge(li, low, mid, high)
快速排序、堆排序、归并排序-小结
- 三种排序算法的时间复杂度都是O(nlogn)
- 一般情况下,就运行时间而言:
- 快速排序 < 归并排序 < 堆排序
- 三种排序算法的缺点:
- 快速排序:极端情况下排序效率低
- 归并排序:需要额外的内存开销
- 堆排序:在快的排序算法中相对较慢
希尔排序思路
- 希尔排序是一种分组插入排序算法。
- 首先取一个整数d1=n/2,将元素分为d1个组,每组相邻量元素之间距离为d1,在各组内进行直接插入排序;
- 取第二个整数d2=d1/2,重复上述分组排序过程,直到di=1,即所有元素在同一组内进行直接插入排序。

- 希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序;最后一趟排序使得所有数据有序。

1 def shell_sort(li): 2 gap = len(li) // 2 3 while gap > 0: 4 for i in range(gap, len(li)): 5 tmp = li[i] 6 j = i - gap 7 while j >= 0 and tmp < li[j]: 8 li[j + gap] = li[j] 9 j -= gap 10 li[j + gap] = tmp 11 gap /= 2
排序-小结
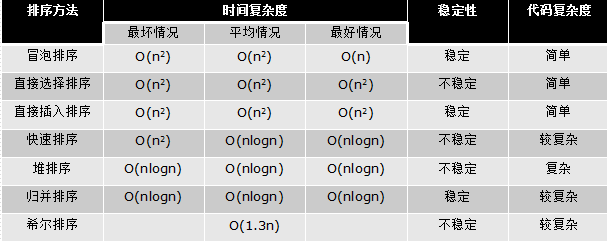
排序-赠品1
- 现在有一个列表,列表中的数范围都在0到100之间,列表长度大约为100万。设计算法在O(n)时间复杂度内将列表进行排序。
- 赠品1-计数排序
-
创建一个列表,用来统计每个数出现的次数。
-
 View Code
View Codedef count_sort(li, max_num): count = [0 for i in range(max_num + 1)] for num in li: count[num] += 1 i = 0 for num,m in enumerate(count): for j in range(m): li[i] = num i += 1
-
排序-赠品2
- 现在有n个数(n>10000),设计算法,按大小顺序得到前m大的数。
- 应用场景:榜单TOP 10
赠品2-堆的应用(了解)
- 解决思路: 取列表前10个元素建立一个小根堆。堆顶就是目前第10大的数。
- 依次向后遍历原列表,对于列表中的元素,如果小于堆顶,则忽略该元素;如果大于堆顶,则将堆顶更换为该元素,并且对堆进行一次调整;
- 遍历列表所有元素后,倒序弹出堆顶。



def topn(li, n): heap = li[0:n] # 建堆 for i in range(n // 2 - 1, -1, -1): sift(heap, i, n - 1) # 遍历 for i in range(n, len(li)): if li[i] > heap[0]: heap[0] = li[i] sift(heap, 0, n - 1) # 出数 for i in range(n - 1, -1, -1): heap[0], heap[i] = heap[i], heap[0] sift(heap, 0, i - 1)
赠品2-堆的应用(了解)
- 优先队列:一些元素的集合,POP操作每次执行都会从优先队列中弹出最大(或最小)的元素。
- 堆——优先队列
- Python内置模块——heapq 利用heapq模块实现堆排序

- 利用heapq模块实现取top-k
-
heapq.nlargest(100, li)
-
算法-习题1
- 给定一个列表和一个整数,设计算法找到两个数的下标,使得两个数之和为给定的整数。保证肯定仅有一个结果。
- 例如,列表[1,2,5,4]与目标整数3,1+2=3,结果为(0, 1).
- https://leetcode.com/problems/two-sum/?tab=Description
算法-习题2
- 给定一个升序列表和一个整数,返回该整数在列表中的下标范围。
- 例如:列表[1,2,3,3,3,4,4,5],若查找3,则返回(2,4);若查找1,则返回(0,0)。
- https://leetcode.com/problems/search-for-a-range/description/
参考博客:https://www.cnblogs.com/liyongsan/p/7788429.html

