函数的定义与使用
可扩展性,可维护性差
代码冗余
可读性差
为什么要用函数+模块化程序设计
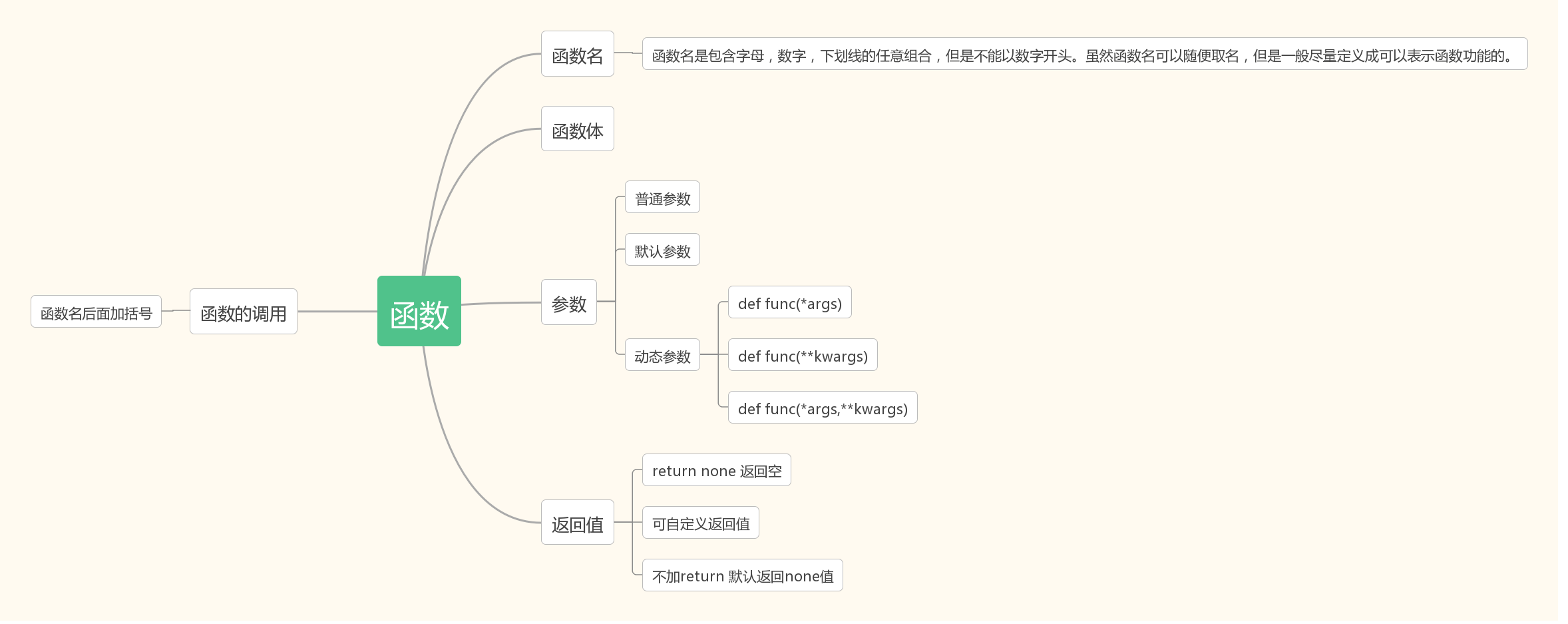
什么是函数?
函数就是具备某一特定功能的工具
函数的使用必须遵循:先定义后使用的原则
先定义就是事先准备号工具
后使用,或者说拿来就用,重复使用,指的就是函数的调用
如何定义函数?
def 函数名(arg1,args2,。。。):
'''注释'''
函数体
return 值
定义函数的三种形式?
无参函数:当函数体内代码无需外部传入参数就可能执行,那就定义成无参函数(通常无需返回值)
def func1():
pass
有参函数:当函数体内代码依赖于外部传入参数才可以执行,那就定义成有参函数(通常需要返回值)
def func2(x):
#print(x)
return x**2
空函数
def func3():
pass
调用函数的形式?
语句形式
func()
表达式
res=func2(10)
res=10*func2(10)
函数调用当做参数传入另外一个函数
res=func2(func2(10))
闭包函数
闭包函数:函数内部定义函数,成为内部函数,
该内部函数包含对外部作用域,而不是对全局作用域名字的引用
那么该内部函数成为闭包函数
闭包函数:1 内部函数 2 包含对外部作用域而非全局作用域的引用
闭包函数的特点:
自带作用域
延迟计算
name='alex'
def func():
def bar():
print(name)
return bar
f=func()
print(f.__closure__)
f()
装饰器
一:开放封闭原则,对扩展是开放的,对修改是封闭的
二:装饰器,装饰器本质可以任意可调用对象,被装饰的对象也可以是任意
可调用对象,
装饰器的功能是:
在不修改被装饰对象源代码以及调用方式的前提下为期添加新功能
原则:
1.不修改源代码
2.不修改调用方法
目标:添加新功能
import time
import random
#装饰器
def timmer(func):
func=index
def wrapper():
start_time = time.time()
func() #index()
stop_time=time.time()
print('run time is %s' %(stop_time-start_time))
return wrapper
#被装饰函数
def index():
time.sleep(random.randrange(1,5))
print('welecome to index page')
def home():
time.sleep(random.randrange(1,3))
print('welecome to HOME page')
index=timmer(index) #index=wrapper
home=timmer(home)
index() #wrapper()
home()
#装饰器的语法:在被装饰对象的正上方的单独一行,@装饰器名字
import time
import random
# #装饰器
def timmer(func):
def wrapper():
start_time = time.time()
func()
stop_time=time.time()
print('run time is %s' %(stop_time-start_time))
return wrapper
# #被装饰函数
@timmer #index=timmer(index)
def index():
time.sleep(random.randrange(1,5))
print('welecome to index page')
@timmer #home=timmer(home)
def home():
time.sleep(random.randrange(1,3))
print('welecome to HOME page')
index() #wrapper()
home()
#加多个装饰器
import time
import random
#装饰器
def timmer(func):
def wrapper():
start_time = time.time()
func()
stop_time=time.time()
print('run time is %s' %(stop_time-start_time))
return wrapper
def auth(func):
def deco():
name=input('name: ')
password=input('password: ')
if name == 'egon' and password == '123':
print('login successful')
func() #wrapper()
else:
print('login err')
return deco
#被装饰函数
@auth #index=auth(wrapper) #index=deco #index=auth(wrapper) #index=deco
@timmer #index=timmer(index) #index=wrapper
def index():
# time.sleep(random.randrange(1,5))
time.sleep(3)
print('welecome to index page')
def home():
time.sleep(random.randrange(1,3))
print('welecome to HOME page')
index() #deco()
home()
#装饰器修订
import time
import random
#装饰器
def timmer(func):
def wrapper(*args,**kwargs):
start_time = time.time()
res=func(*args,**kwargs)
stop_time=time.time()
print('run time is %s' %(stop_time-start_time))
return res
return wrapper
#被装饰函数
@timmer
def index():
time.sleep(random.randrange(1,5))
print('welecome to index page')
@timmer
def home(name):
time.sleep(random.randrange(1,3))
print('welecome to %s HOME page' %name)
return 123123123123123123123123123123123123123123
index()
res1=index()
print('index return %s' %res1)
res2=home('egon') #wraper()
print('home return %s' %res2)