浅谈JMM

概述

JMM的全称是Java Memory Model（Java内存模型）

JMM的关键技术点都是围绕着多线程的原子性、可见性和有序性来建立的，这也是Java解决多线程并行机制的环境下，定义出的一种规则，意在保证多个线程间可以有效地、正确地协同工作。

三要素

原子性（Atomicity）

原子性是指一个操作是不可中断的，即使是在多个线程一起执行的情况下，一个操作一旦开始执行，就不会受到其他线程的干扰。

比如，有两个线程同时对一个静态全局变量int num进行赋值，线程A给他赋值为1，线程B给他赋值为2，那么不管这两个线程以何种方式何种步调去执行，num的值最终要么是1要么是2，线程A和线程B在赋值操作期间，是不可能受到对方干扰的，这就是原子性的一个特点——不可被中断。

但如果我们不使用int类型而是用long类型的话，可能就会出现差池了，因为对于32位系统来说，long类型数据的写入不是原子性的（因为long有64位），也就是说，如果两个线程在32位操作系统下同时对一个long类型的数据进行同步操作，那么线程之间的数据操作可能是有干扰的。

可见性（Visibility）

可见性是指在多线程情况下，当一个线程修改了某一个共享变量的值之后，其他线程是否能够立即知道这个修改。显然，对于串行线程来说，可见性问题是不存在的，因为你在任何一个操作步骤中修改了某个变量的值，那么在后续步骤中，读取这个变量的值，一定是修改后的新值。

但是这个问题在并行程序中就不见得了。

如果一个线程修改了某一个全局变量，那么其他线程未必能够马上知道这个改动，如下图便展示了可见性问题的一种可能：

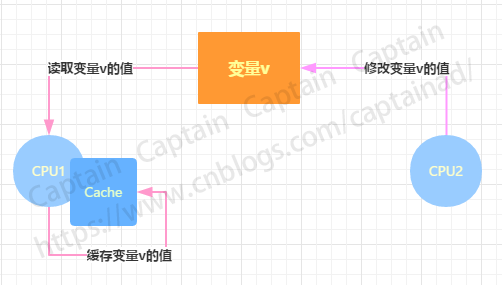
如果在CPU1和CPU2上各运行一个线程，它们共享变量v，由于编译器优化或者硬件优化的缘故，在CPU1上对变量v进行了优化，将这个值拷贝缓存到cache或者寄存器中，这种情况下，如果在CPU2上的某个线程修改了变量v的实际值，那么CPU1上的线程可能无法感知这个改动，依然会读取之前拷贝到cache或者寄存器里的数据进行操作，因此这就产生了可见性问题。外在表现为：变量v的值被修改了，但是CPU1上的线程依然会读到一个修改之前的旧值。可见性问题也是并行程序开发中需要哪个重点关注的问题之一。

可见性问题是一个综合性问题，除了上述提到的缓存优化或者硬件优化（有些内存读写可能不会立即出发，而是先进入到一个硬件队列等待）会导致可见性问题外，指令重排以及编译器优化等，都有可能导致一个线程的修改不会立即被其他线程所察觉到。

有序性（Ordering）

有序性问题可能是比较难理解的一个问题。对于一个线程执行的代码而言，我们总是习惯地认为代码总是按照书写顺序从先往后依次执行，这在单线程环境下，确实如此，但是在多线程并发环境下估计就不见得了，程序的执行可能就会出现乱序，给人的感觉就是写在前面的代码可能在后面执行了。其实有序性问题的原因是因为程序在执行时，可能因为编译器优化的缘故，进行了指令重排的操作，重排后的指令与原指令的顺序未必一致。

我们上面的叙述都是以不确定的口吻来表达的，我们都说是这种情况下可能存在，因为如果没有指令重排的现象发生，问题就不存在了，但是指令重排是否发生、如何进行指令重排、何时进行指令重排，我们不得而知也无法预测。因此对于这类问题，我们比较严谨的描述就是：线程A的指令执行顺序在线程B看来是没有保证的，如果运气好，线程B也许真的可以看到和线程A一样的执行顺序。

不过这里我们还需要强调一点，对于一个线程来说，它看到的指令执行顺序一定是一致的，也就是说指令重排是有个一基本前提的，就是必须保证串行语义的一致性，不管指令怎么重排序都不会使串行的语义逻辑发生问题。

注意：指令重排可以保证串行语义一致，但是没有义务保证多线程间的语义也一致。

那么为什么要指令重排呢？

之所以这么做，完全是基于代码执行的性能考虑的。我们知道，一条指令的执行是分多个步骤的，简单的说，可以分为以下几步：

1. 取指 IF
2. 译码和取寄存器操作数 ID
3. 执行或者有效地址计算 EX
4. 存储器访问 MEM
5. 写回 WB

我们的汇编指令也不是一步就执行完成的，在CPU中实际工作时，它还是需要分多个步骤依次执行的。当然，每个步骤所涉及的硬件也可能不同，比如取值时会用到PC寄存器和存储器，译码时会用到指令寄存器组，执行时会使用ALU，写回时需要寄存器组。

由于每一个步骤都可能使用不同的硬件来完成，因此，聪明的工程师们发明了流水线技术来执行指令，如下图所示的工作原理：

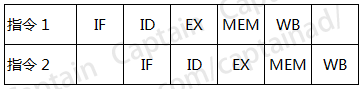
可以看到，当第二条指令执行时，第一条指令其实并未执行完，确切地说是第一条指令还没有开始执行，只是完成了取指的操作而已。这样的好处就非常明显了，假如这里每一个步骤都需要花费1毫秒，那么指令2等待指令1完全执行后再执行，则需要等待5毫秒的时间，而是用这种流水线模式后，指令2就只需要等待1毫秒的时间就可以开始执行了，这样以来就带来了很大的性能提升，在商业环境中这种流水线级别甚至更高，性能提升就愈加的明显了。

有了流水线这种模式，我们的CPU才能真正更高效的运行，但是，流水线总是害怕被迫中断。流水线满载时性能是很高的，但是一旦中断，所有的硬件设备就会进入到停顿器，等到再次满载运行就又要等到几个周期，因此性能损失会很大，所以我们必须想办法不让流水线中断。

那么答案就来了，之所以需要做指令重排，就是为了尽量减少指令流水线执行时的中断。当然了，指令重排只是减少中断的一种技术，实际上在CPU涉及中，还有更多的软硬件技术来防止中断，这里就不做更多叙述了。

为了加深对指令重排序的认识，理解指令重排序对性能提升的意义，我们通过一些简单的例子来增加感性的认识。

下图展示了A=B+C这个操作的执行过程，写在左边的是汇编指令，其中LW表示load加载，LW R1,B就是表示将B的值加载到R1寄存器当中，ADD是加法，LW R3,R1,R2就是表示将R1R2的值相加并存放到R3中，SW表示存储，SW A,R3就是表示将R3寄存器的值保存到变量A中。

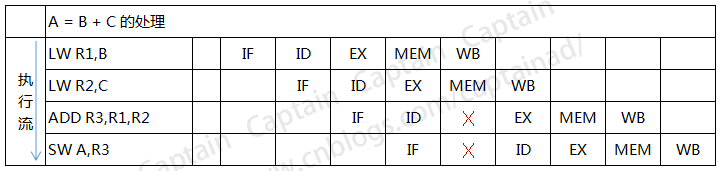
（A=B+C的执行过程，图标仿自书籍）

右边就是流水线的情况，其中在ADD指令上就有一个大X，这就表示一个中断，为什么这里会有中断（停顿）呢？原因很简单，R2中的数据还没有准备好，必须要等到它写回到存储器上才能继续使用，所以ADD操作在这里必须等待一次。由于ADD的延迟，导致其后面所有的指令都要慢一步。

我们可以再来看一个稍微更复杂一点的例子：

a = b + c

d = e - f

上述代码的执行应该会是这样的，如下图所示：

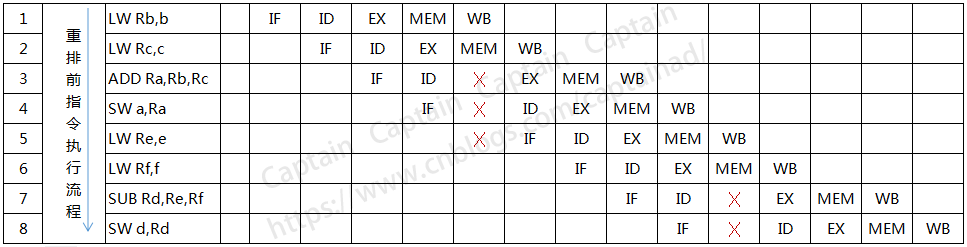
从上图我们可以看出，由于ADD和SUB操作都需要等待上一条指令的结果，所以插入了不少的停顿，那么对于这段代码，我们是否可以消除这些停顿呢，显然是可行的。我们只需要将LW Re,e和LW Rf,f的操作移动到前面去执行即可，思路很简单，就是先加载e和f对程序执行是没有影响的，因为既然ADD的时候要停顿一下，那么不如将停顿的时间去用来做点别的操作。

针对上面的指令流程，我们将第5条指令挪到第2条指令的后面执行，将第6条指令挪到上图的第3条指令后面去执行，于是我们重新画一下指令重排后的执行流程图，如下所示：

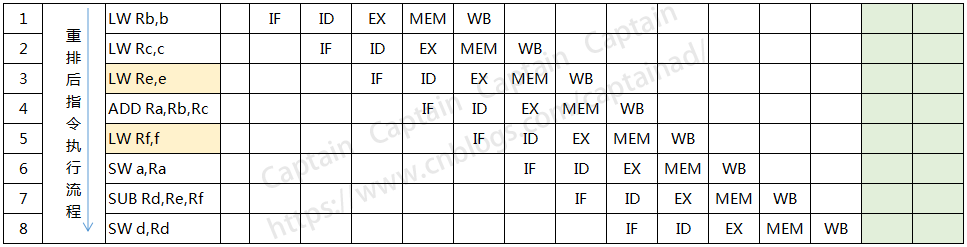
上面这块代码的运算流程，在指令重排后减少了2次停顿，对于提高CPU处理性能效果明显，由此可见，指令重排对于提高CPU处理器性能还是十分必要的，虽然确实带来了乱序的问题，但是这点牺牲完全是值得的。

Happen-Before规则

上面介绍了指令重排，虽然Java虚拟机和执行系统会对指令进行一定的重排，但是指令重排是有原则的，并发所有的指令都可以随便更改执行位置，下面罗列了一些基本原则，这些原则是指令重排不可以违背的：

• 程序顺序原则：一个线程内保证语义的串行性
• volatile规则：volatile变量的写操作，先发生于读操作，这保证了volatile变量的可见性
• 锁规则：解锁（unlock）必然发生在随后的加锁（lock）前
• 传递性：A先于B，B先于C，那么A必然先于C
• 线程的start()方法先于它的每一个动作
• 线程的所有操作先于线程的终结（Thread.join()）
• 线程的中断（interrupt）先于被中断线程的代码
• 对象的构造函数执行、结束先于finalize()方法

以程序顺序原则为例，重排后的指令绝对不能改变原有的串行语义，比如：

a = 1

b = a + 1

由于第二条语句依赖第一条语句执行的结果，如果冒然交换两条代码的执行顺序，那么程序的语义就会被修改，因此这种情况是绝对不允许发生的，这也是指令重排必须遵循的第一条基本原则。

此外，锁规则强调，unlock操作必然发生在后续对同一把锁的lock之前。也就是说，如果对一个锁的解锁后再加锁，那么加锁的执行动作绝对不可能重排到解锁的动作之前，很显然如果这么做，加锁就没有意义了。

其他几条原则也类似，都是为了保证指令重排不会破坏原有的语义结构。

参考资料

1、实战Java高并发程序设计 / 葛一鸣，郭超编著. —北京：电子工业出版社，2015.11