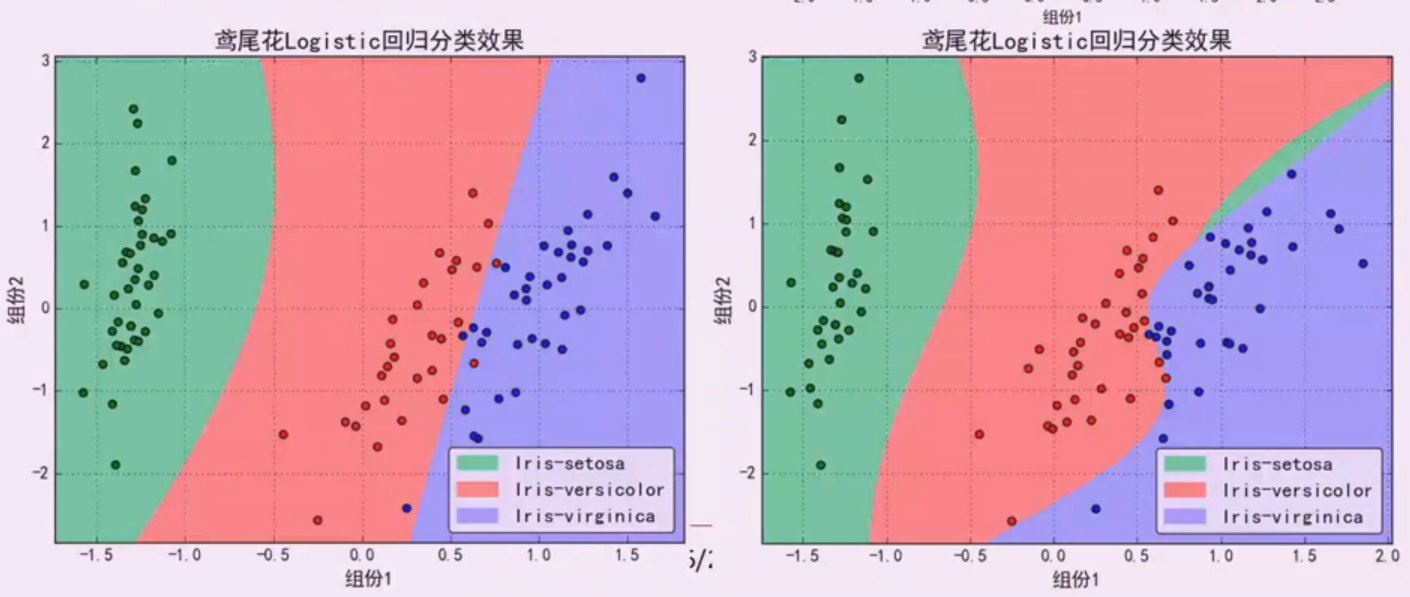
对鸢尾花数据集采用主成分分析方法,使数据降维。
如下图所示为数据集的格式:
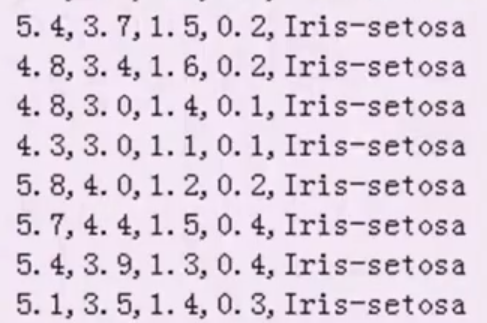
数据集中前4列数据分别代表花萼长度,花萼宽度,花瓣长度,花瓣宽度,最后一列为标签。共有150条数据。
我们对此数据集利用主成分分析方法,取出数据集的前4列特征组成矩阵X, 矩阵X的维度为150*4,对其进行转置后变为4*150.
第二步用X.T*X得到4*4维度的对称矩阵,我们就可以求这个对称矩阵的特征值lambda1,lambda2,lambda3,lambda4和对应的特征向量u1,u2,u3,u4。特征值一定是实数,特征向量之间是相互正交的。每个特征向量都是4*1的向量。
第三步把特征值做一个从大到小的排列,取出前两个最大的特征值和对应的特征向量。如果说lambda1最大,也就是说u1是最主要的方向,是最主要的主成分。次大的特征值对应的特征向量是第二主成分,依次往下排列。
假如说u1,u2是排列前2的主成分,那么就把样本数据都投影到u1和u2这个方向上,这是只有两维的数据了,并且u1,u2还是垂直的。可以把他看成新的特征选择或组合。效果如下:
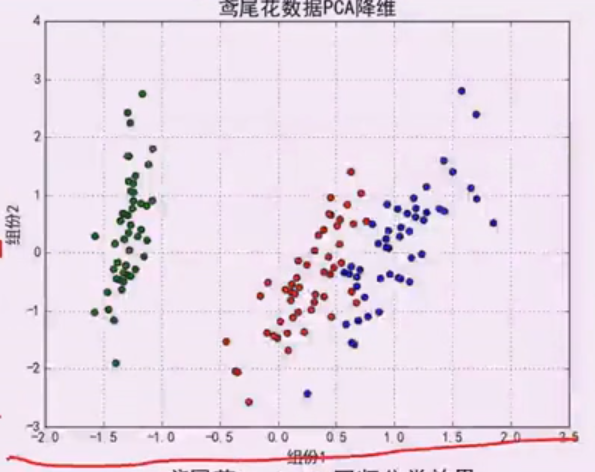
由上图可知,投影后的数据可以很容易的对其进行分类。如下图所示: