LeetCode 69 题

1.题目要求

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2

示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 
     由于返回类型是整数，小数部分将被舍去。

2.初次尝试

这道题很明显不是让我们调用 Math.sqrt() 方法来计算，而是自己实现一个求平方根的算法。第一反应想到的方法是暴力循环求解！从 1 开始依次往后求平方数，当平方数等于 x 时，返回 i ；当平方数大于 x 时，返回 i - 1。

class Solution {
    public int mySqrt(int x) {
        for(int i = 0; i <= x; i++) {
            if(i * i >= x){
                if(i * i == x)
                    return i;
                else
                    return i - 1;
            }
        }
        return 0;
    }
}

这种方案通过了测试，但是成绩惨不忍睹：

执行用时 : 105 ms, 在Sqrt(x)的Java提交中击败了5.53% 的用户
内存消耗 : 33.1 MB, 在Sqrt(x)的Java提交中击败了83.60% 的用户

好奇心驱使下，我用了 Math.sqrt() 方法又提交了一遍答案：

class Solution {
    public int mySqrt(int x) {
        return (int)Math.sqrt(x);
    }
}

成绩有点无解：

执行用时 : 5 ms, 在Sqrt(x)的Java提交中击败了99.24% 的用户
内存消耗 : 33.2 MB, 在Sqrt(x)的Java提交中击败了80.86% 的用户

这样一道乍看之下有点“蠢”的题目，其实有很多可以深究的地方。Math.sqrt() 用的是什么算法？求平方数的算法还有哪些？

Google 了一下“求平方根”，看到了两个出镜率最高的名词，一个是我们耳熟能详的“二分法”，另一个则是我第一次听说的“牛顿迭代法“。难得五一假期有空，决定了解一下”牛顿迭代法“并自己写出基于此算法的解题答案。

3.牛顿迭代法

我是根据知乎上一个回答了解牛顿迭代法的，链接贴出来了，有兴趣的朋友可以移步去看一下。这里简单的通过他的文章说明一下思路。

如何通俗易懂地讲解牛顿迭代法求开方？数值分析？​www.zhihu.com

这种算法的一个重要的思想是：切线是曲线的线性逼近。基于这种思想，牛顿尝试用切线来研究曲线的问题，例如用切线的根近似的求出曲线的根。然后他观察到一个现象，当在曲线上取某一点作切线时，以该切线的根作垂线，在垂线和曲线的交点处再作切线，以此循环往复，切线的根逐渐会逼近曲线的根。如图所示（A点时第一个取的点）。

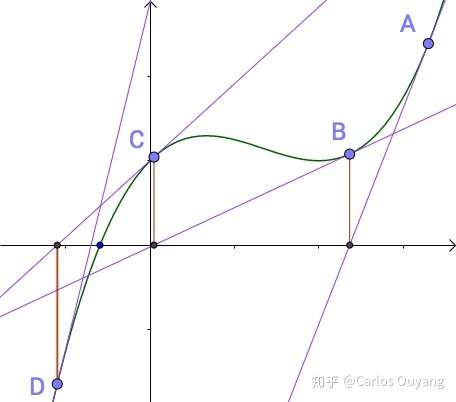
当然，其实这种迭代并不是一定能保证会向曲线的根逼近，具体原因可以移步上述链接。但是求二次方程的根是没有问题的。

4.牛顿迭代法求平方根

回归到题目，求 a 的平方根，实际上可以转换成求二次方程 x^2 - a = 0 的解的问题。然后可以作出该二次方程的曲线，通过迭代逼近曲线 y = 0 处 x 的值，该 x 即是需要求得的答案。提现到程序中如下：

class Solution {
    public int mySqrt(int x) {
        if(x == 1)
            return 1;
        double _x = x >> 1;
        double _y = _x * _x - x;
        double a = (-_y + 2 * _x * _x) / 2 / _x;
        while(_y > 0.1 || _y < -0.1){
            _x = a;
            _y = _x * _x - x;
            a = (-_y + 2 * _x * _x) / 2 / _x;
        }
        return (int)_x;
    }
}

这个程序很直观的反应了迭代的过程，"_x" 是二次方程的横坐标，"_y" 是方程的纵坐标，"a" 是切线与 x 轴的交点处的横坐标。选取的第一点为 x / 2 作为横坐标，当 _y 的值逼近 0 的时候，返回 _x。该方法的成绩很接近 Math.sqrt()，结果为：

执行用时 : 6 ms, 在Sqrt(x)的Java提交中击败了92.91% 的用户
内存消耗 : 33.7 MB, 在Sqrt(x)的Java提交中击败了75.11% 的用户

5.简化

这里其实可以注意到，该二次方程一定是关于 y 轴对称的，而且二次方程在迭代过程中，若初始点在根的右边，则迭代的点会一直出现在根的右边，且一直逼近根。我们要找的其实是比根小的最大的整数，可以把 a 换成 int 类型，在逼近过程中，当 a 第一次小于等于 x / a 时，返回 a。

对程序进行简化，去掉一些不必要的参数，优化最后判断足够逼近的方式，最后程序为：

class Solution {
    public int mySqrt(int x) {
        if(x == 1 || x == 0)
            return x;
        int a = x >> 1;
        while(a > x / a){
            a = (a + x/a) / 2;
        }
        return a;
    }
}