【计算机视觉】OpenCV篇(6)

平滑滤波

平滑滤波是低频增强的空间域滤波技术。空间域滤波技术即不经由傅立叶转换，直接处理影像中的像素，它的目的有两类：一类是模糊；另一类是消除噪音。空间域的平滑滤波一般采用简单平均法进行，就是求邻近像元点的平均亮度值。邻域的大小与平滑的效果直接相关，邻域越大平滑的效果越好，但邻域过大，平滑会使边缘信息损失的越大，从而使输出的图像变得模糊，因此需合理选择邻域的大小。-- 整理自《维基百科》与《百度百科》

滤波 VS 模糊 

 关于滤波和模糊：

• 它们都属于卷积，不同滤波方法之间只是卷积核不同（对线性滤波而言）
• 低通滤波器是模糊，高通滤波器是锐化

 低通滤波器就是允许低频信号通过，在图像中边缘和噪点都相当于高频部分，所以低通滤波器用于去除噪点、平滑和模糊图像。高通滤波器则反之，用来增强图像边缘，进行锐化处理。

【注：常见的噪声有椒盐噪声和高斯噪声，椒盐噪声可以理解为斑点，随机出现在图像中的黑点或白点；高斯噪声可以理解为拍摄图片时由于光照等原因造成的噪声。】

滤波的方式有很多种，下面介绍一些常用的：

（1）均值滤波（Mean Filter）

均值滤波是一种最简单的滤波处理，它取的是卷积核区域内元素的均值，3×3的卷积核实现如下：

img = cv2.imread('../images/lena.jpg')
# 均值滤波
blur = cv2.blur(img, (3, 3))

 典型特点：可以去除均匀噪声和高斯噪声，但会对图像造成一定程度的模糊，而且使用的窗口越大，造成的模糊也就越明显。　

（2）方框滤波(Box Filter)

方框滤波跟均值滤波很像，3×3的滤波核如下：

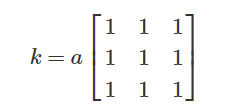
当可选参数normalize为True的时候，方框滤波就是均值滤波，上式中的a就等于1/9；normalize为False的时候，a=1，相当于求区域内的像素和。

# 前面的均值滤波也可以用方框滤波实现：normalize=True
blur = cv2.boxFilter(img, -1, (3, 3), normalize=True)

（3）高斯滤波(Gaussian Filter)

前面两种滤波方式，卷积核内的每个值都一样，也就是说图像区域中每个像素的权重也就一样。高斯滤波的卷积核权重并不相同：中间像素点权重最高，越远离中心的像素权重越小，还记得标准正态分布的曲线吗？

显然这种处理元素间权值的方式更加合理一些。如果图像是2维的，那么就需要使用二维高斯函数：

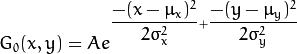
其中 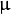 为均值 (峰值对应位置)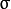，  代表标准差 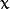(变量  和 变量 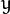 各有一个均值，也各有一个标准差)

# 均值滤波vs高斯滤波
img = cv2.imread('../images/gaussian_noise.bmp')
blur = cv2.blur(img, (5, 5))  # 均值滤波
gaussian = cv2.GaussianBlur(img, (5, 5), 1)  # 高斯滤波

 其中，参数3 σx值越大，模糊效果越明显。高斯滤波相比均值滤波效率要慢，但可以有效消除高斯噪声，能保留更多的图像细节，所以经常被称为最有用的滤波器。均值滤波与高斯滤波的对比结果如下（均值滤波丢失的细节更多）：　　

 

（4）中值滤波(Median Filter)

中值又叫中位数，是所有数排序后取中间的值。中值滤波就是用区域内的中值来代替本像素值，所以那种孤立的斑点，如0或255很容易消除掉，适用于去除椒盐噪声和斑点噪声。中值是一种非线性操作，效率相比前面几种线性滤波要慢。

比如下面这张斑点噪声图，用中值滤波显然更好：

# 均值滤波vs中值滤波
img = cv2.imread('../images/salt_noise.bmp', 0)

blur = cv2.blur(img, (5, 5))  # 均值滤波
median = cv2.medianBlur(img, 5)  # 中值滤波

（5）双边滤波（Bilateral Filter）

模糊操作基本都会损失掉图像细节信息，尤其前面介绍的线性滤波器，图像的边缘信息很难保留下来。然而，边缘（edge）信息是图像中很重要的一个特征，为避免在削弱噪声时连带着磨掉边缘的情形 (至少在一定程度上 ), 我们可以使用双边滤波。。　

# 双边滤波vs高斯滤波
img = cv2.imread('../images/lena.jpg', 0)
gau = cv2.GaussianBlur(img, (5, 5), 0)  # 高斯滤波
blur = cv2.bilateralFilter(img, 5, 75, 75)  # 双边滤波

【双边滤波明显保留了更多边缘信息】

总结

• 在不知道用什么滤波器好的时候，优先高斯滤波cv2.GaussianBlur()，然后均值滤波cv2.blur()
• 斑点和椒盐噪声优先使用中值滤波cv2.medianBlur()
• 要去除噪点的同时尽可能保留更多的边缘信息，使用双边滤波cv2.bilateralFilter()
• 线性滤波方式：均值滤波、方框滤波、高斯滤波（速度相对快）
• 非线性滤波方式：中值滤波、双边滤波（速度相对慢）

　　

附录 -- 全篇Python源代码：

import cv2
import numpy as np

img = cv2.imread('../images/lena.jpg')
# 1.均值滤波
blur = cv2.blur(img, (3, 3))
blur2 = cv2.blur(img, (7, 7)) #使用不同大小的滤波核（滑动窗口）

# 上面的均值滤波也可以用方框滤波实现：normalize=True
# blur = cv2.boxFilter(img, -1, (3, 3), normalize=True)

# 2.高斯滤波
gau_blur = cv2.GaussianBlur(img, (3, 3), 0)

# 四张图片横向叠加对比显示
res = np.hstack((img, blur, blur2, gau_blur))
cv2.imshow('res', res)
cv2.waitKey(0)

# 均值滤波vs高斯滤波
img = cv2.imread('../images/gaussian_noise.bmp')
blur = cv2.blur(img, (5, 5))  # 均值滤波
gaussian = cv2.GaussianBlur(img, (5, 5), 1)  # 高斯滤波

res = np.hstack((img, blur, gaussian))
cv2.imshow('gaussian vs average', res)
cv2.waitKey(0)


# 3.均值滤波vs中值滤波
img = cv2.imread('../images/salt_noise.bmp', 0)

blur = cv2.blur(img, (5, 5))  # 均值滤波
median = cv2.medianBlur(img, 5)  # 中值滤波

res = np.hstack((img, blur, median))
cv2.imshow('median vs average', res)
cv2.waitKey(0)


# 4.双边滤波vs高斯滤波
img = cv2.imread('../images/lena.jpg', 0)
gau = cv2.GaussianBlur(img, (5, 5), 0)  # 高斯滤波
blur = cv2.bilateralFilter(img, 5, 75, 75)  # 双边滤波

res = np.hstack((img, gau, blur))
cv2.imshow('res', res)
cv2.waitKey(0)

OpenCV4.1.0 C++ Smoothing Sample Code:

/**
 * file Smoothing.cpp
 * brief Sample code for simple filters
 * author OpenCV team
 */

#include <iostream>
#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"

using namespace std;
using namespace cv;

/// Global Variables
int DELAY_CAPTION = 1500;
int DELAY_BLUR = 100;
int MAX_KERNEL_LENGTH = 31;

Mat src; Mat dst;
char window_name[] = "Smoothing Demo";

/// Function headers
int display_caption( const char* caption );
int display_dst( int delay );


/**
 * function main
 */
int main( int argc, char ** argv )
{
    namedWindow( window_name, WINDOW_AUTOSIZE );

    /// Load the source image
    const char* filename = argc >=2 ? argv[1] : "../data/lena.jpg";

    src = imread( filename, IMREAD_COLOR );
    if(src.empty())
    {
        printf(" Error opening image
");
        printf(" Usage: ./Smoothing [image_name -- default ../data/lena.jpg] 
");
        return -1;
    }

    if( display_caption( "Original Image" ) != 0 )
    {
        return 0;
    }

    dst = src.clone();
    if( display_dst( DELAY_CAPTION ) != 0 )
    {
        return 0;
    }

    /// Applying Homogeneous blur
    if( display_caption( "Homogeneous Blur" ) != 0 )
    {
        return 0;
    }

    //![blur]
    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        blur( src, dst, Size( i, i ), Point(-1,-1) );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }
    //![blur]

    /// Applying Gaussian blur
    if( display_caption( "Gaussian Blur" ) != 0 )
    {
        return 0;
    }

    //![gaussianblur]
    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        GaussianBlur( src, dst, Size( i, i ), 0, 0 );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }
    //![gaussianblur]

    /// Applying Median blur
    if( display_caption( "Median Blur" ) != 0 )
    {
        return 0;
    }

    //![medianblur]
    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        medianBlur ( src, dst, i );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }
    //![medianblur]

    /// Applying Bilateral Filter
    if( display_caption( "Bilateral Blur" ) != 0 )
    {
        return 0;
    }

    //![bilateralfilter]
    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        bilateralFilter ( src, dst, i, i*2, i/2 );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }
    //![bilateralfilter]

    /// Done
    display_caption( "Done!" );

    return 0;
}

/**
 * @function display_caption
 */
int display_caption( const char* caption )
{
    dst = Mat::zeros( src.size(), src.type() );
    putText( dst, caption,
             Point( src.cols/4, src.rows/2),
             FONT_HERSHEY_COMPLEX, 1, Scalar(255, 255, 255) );

    return display_dst(DELAY_CAPTION);
}

/**
 * @function display_dst
 */
int display_dst( int delay )
{
    imshow( window_name, dst );
    int c = waitKey ( delay );
    if( c >= 0 ) { return -1; }
    return 0;
}　　

　　

　　

引用参考：

图像平滑处理

Smoothing Images