优点:
在数据预处理时首先可以对偏度比较大的数据用log1p函数进行转化,使其更加服从高斯分布,此步处理可能会使我们后续的分类结果得到一个更好的结果;
平滑处理很容易被忽略掉,导致模型的结果总是达不到一定的标准,同样使用逼格更高的log1p能避免复值的问题——复值指一个自变量对应多个因变量;
log1p的使用就像是将一个数据压缩到了一个区间,与数据的标准化类似。下面再说说它的逆运算expm1函数。
由于前面使用过log1p将数据进行了压缩,所以最后需要记得将预测出的平滑数据进行一个还原,而还原过程就是log1p的逆运算expm1。
上面介绍了两者的概念和方法的优点,下面说说具体的数学含义:
log1p和expm1的功能:
log1p := log(x+1) 即 ln(x+1)
expm1 := exp(x)-1
log1p函数有它存在的意义,即保证了x数据的有效性,当x很小时(如e-16),由于太小超过数值有效性,用log(x+1)计算得到结果为0,换作log1p则计算得到一个很小却不为0的结果,这便是它的意义。
同样的道理对于expm1,当x特别小,就会急剧下降出现如上问题,甚至出现错误值。
推导:
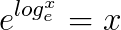
均方根对数误差(RMSLE):
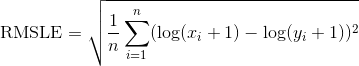
RMSLE会更多的惩罚欠拟合,所以在使用该误差定义时我们也可以用到上面的函数:
np.loglp计算加一后的对数,其逆运算是np.expm1;
采用此误差函数时,可以先对原始数据做np.log1p,再使用RMSE。